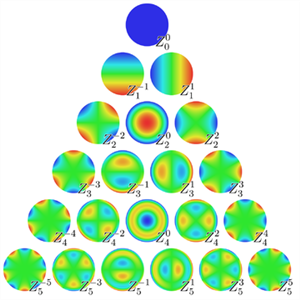
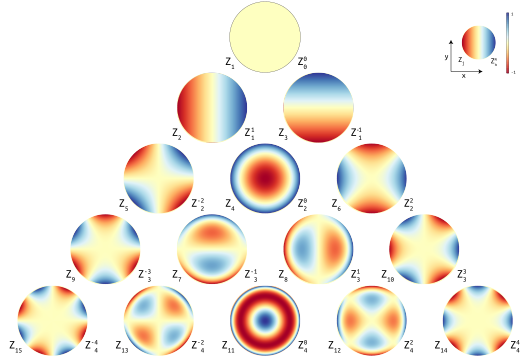
泽尔尼克多项式是一个以1953年获诺贝尔物理学奖荷兰物理学家弗里茨·泽尔尼克命名的正交多项式，分为奇、偶两类
齐多项式：
-
Z n m ( ρ , φ ) = R n m ( ρ ) cos ( m φ ) {\displaystyle Z_{n}^{m}(\rho ,\varphi )=R_{n}^{m}(\rho )\,\cos(m\,\varphi )\!}
偶多项式
-
Z n − m ( ρ , φ ) = R n m ( ρ ) sin ( m φ ) , {\displaystyle Z_{n}^{-m}(\rho ,\varphi )=R_{n}^{m}(\rho )\,\sin(m\,\varphi ),\!}
其中 n ≥ m {\displaystyle n\geq m} 
为非负整数，
ϕ {\displaystyle \phi } 
为方位角
0
≤
ρ
≤
1
{\displaystyle 0\leq \rho \leq 1}
为径向距离
如果 n-m为偶数则
-
R n m ( ρ ) = ∑ k = 0 n − m 2 ( − 1 ) k ( n − k ) ! k ! ...
