应用

在物理学，天文学，与流体力学里，速端曲线可以用来绘示物质的形变，行星的运动，以及任何涉及物体速度的数据。

气象学

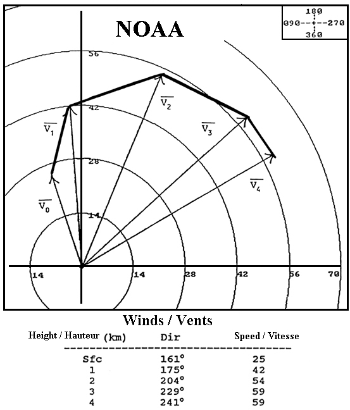
用无线电探空仪搜集的高空气流数据绘出的速端曲线（资料来源：美国国家海洋和大气管理局）。

在气象学里，无线电探空仪搜集的高空气流数据，可以用速端曲线来展示。采用极线图。以参考轴为一边测量出来的角度代表风向，而径向距离则代表风强度。如右图下方的数据列表显示，在五种不同高度的气层的风向与风强度 。这些风的数据，矢量 V0{\displaystyle \mathbf {V} _{0}} 至 V4{\displaystyle \mathbf {V} _{4}} ，都已被绘于图内。说明方向的资料显示于图右上角。

有了速端曲线与各种热力学绘图 (thermodynamic diagram) ，像温熵图 (tephigram)，气象学家可以计算出

风切变：每一个矢量与其相邻矢量的首部连线，可以显示出，在那一层大气层内的方向与强度的变化。对于雷暴的发展和风的未来演变，风切变给予我们很重要的资料。

湍流:风切变意味着可能会有湍流存在。湍流时常会对于飞机航空造成危险。

温度平流：用某一个气层的风向资料与其上面气层的风切变资料，可以计算出这一个气层的空气温度改变。在北半球，假设两个气层之间存在着风切变，则其右边必有暖空气的存在。相反现象会发生在南半球（参阅热力风 (thermal wind) ）。如上图，从西南方吹来的风 V3{\displaystyle \mathbf {V} _{3}} 与风切变的右边相会，这意味着暖平流 (advection) ，在那气层的空气会变暖。

参阅

拉普拉斯-龙格-楞次矢量

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。