Fibonacci LFSRs

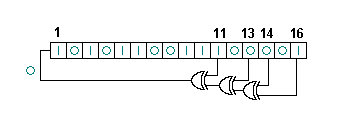
  一个 16-位 Fibonacci LFSR. 图中白色数字为抽头，与表中本原多项式相对应，则寄存器的循环周期为最大，65535（不包括全零状态）。图中的状态为 0xACE1 (十六进制) 下一个状态是 0x5670.

影响下一个状态的比特位叫做抽头。图中，抽头序列为[16,14,13,11]。LFSR最右端的比特为输出比特。抽头依次与输出比特进行异或运算，然后反馈回最左端的位。最右端位置所生成的序列被称为输出流。

影响LFSR下一个状态的比特位叫做抽头（图中白色数字）

最大长度的LFSR生成一个M序列（例如，只有与有一定抽序列的LFSR才能通过所有 2 − 1 个内部状态，不包括全零状态），除非它本身为全零，亦即状态永不改变

作为基于异或运算的LFSR的替换，LFSR也可以给予同或运算。与使用异或门的LFSR全零状态下为无效状态相应的，使用同或门的LFSR在全“1”状态下也是无效的。

有LFSR或者基于同或门的LFSR生成的序列可以被认为是通格雷码或者自然二进制码同样有效的二进制序列。

在LFSR中，抽头的设定可以用有限域算数中模2的多项式来表示。这就意味着，多项式中的所有系数必须是“1”或者“0”。这个多项式被称作回授多项式或特征多项式。例如图中的抽头为在第16，14，13，11个比特，则相应的特征多项式为：

多项式中常数“1”并不代表某一个抽头，它所指的是一个比特位的输入（例如 x,等效为 1 ）。多项式中的指数代表从左至右的抽头位。第一个和最后一个比特一般相应的是输入和输出位。

当且仅当相应的回授多项式是本原多项式时，LFSR才能达到最大长度。这表示一下条件是必须的：

抽头的数量必须为偶数。

抽头之间不能成对出现，必须是互质的。

生成最长LFSRs的本原多项式表可通过的链接找到。 这类型LFSR也被成为标准，多对一或外部异或门的LFSR。下一节将会介绍Galois型的LFSR。

Galois LFSRs

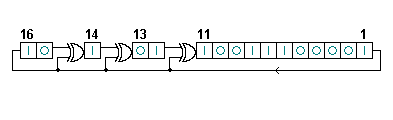
  A 16-bit Galois LFSR. The register numbers in white correspond to the same primitive polynomial as the Fibonacci example but are counted in reverse to the shifting direction. This register also cycles through the maximal number of 65535 states excluding the all-zeroes state. The state ACE1 hex shown will be followed by E270 hex.

以法国数学家埃瓦里斯特·伽罗瓦命名，是LFSRs的Galois型结构。

参见

梅森旋转算法

M-sequence

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。