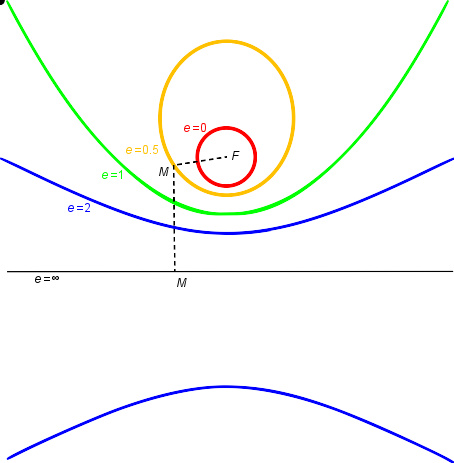
轨道离心率
计算
轨道离心率能够从轨道状态向量计算得知离心率向量的大小:
此处:
e {\displaystyle \mathbf {e} \,\!} 是离心率向量。
对椭圆轨道也能从距离的近拱点和远拱点计算得知:
此处:
d p {\displaystyle d_{p}\,\!} 是近拱点的距离。
d a {\displaystyle d_{a}\,\!} 是远拱点的距离。
举例
例如,地球现在的轨道离心率是0.0167,而由于行星间的重力吸引,经过一段时间会慢慢变成接近0,而最大值约为0.05。(图请参考[1])。
在其他的数值上,水星的离心率(0.2056)是在太阳系内行星中最大的。在2006年行星重定义,矮行星的冥王星有更大的离心率大约0.248,月球有值得注意的离心率0.0554。其他行星的离心率,可以参考 太阳系的行星表 。
对气候的影响
季节的长度对应于地球在轨道上经过分点与至点间所扫掠过的面积。
轨道力学要求季节长度需要与对应季节的象限被扫掠过的面积成比率,所以在轨道离心率的极值,在远心点上的时间(日期)会比在近心点上要长。今天,在北半球,在秋季与冬季位于近日点附近,地球以最快的速度运动着,因此冬季和秋季比春季和夏季为短。在2006年,北半球的夏天比冬天长4.66天,春天比秋天长2.9天。(source)轴向进动缓缓的改变地球的分点与至点在轨道上的位置,参考回归年有更详细的说明与数值。在未来的10,000年,北半球的冬季会逐渐变长,而夏季会变得短些,最后,创造出来的环境将顺理成章的引发下一次的冰河期。
相关条目
离心向量
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








24小时热门
推荐阅读
关于我们

APP下载




























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}