概念

“理想刚体”是一种有限尺寸，可以忽略形变的固体。不论是否感受到外力，在刚体内部，点与点之间的距离都不会改变。根据相对论，这种物体不可能实际存在，但物体通常可以假定为完美刚体，前提是必须满足运动速度超小于光速的条件。

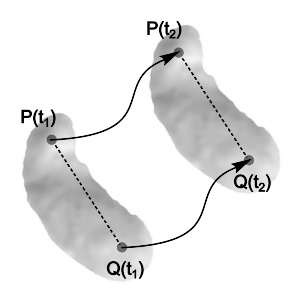
  一个刚体在做平移运动。

如右图所示，从时间 t 1 {\displaystyle t_{1}} 到时间 t 2 {\displaystyle t_{2}} ，当刚体在做平移运动时，任意内部两点，点P与点Q的轨迹（以黑色实线表示）相互平行，线段 P Q ¯ ¯ --> {\displaystyle {\overline {PQ}}} （以黑色虚线表示）的方向保持恒定、长度不会改变。

挑选刚体内部一点G来代表整个刚体，则在刚体内部任意一点P的位置 r P {\displaystyle \mathbf {r} _{P}} 为

其中， r G {\displaystyle \mathbf {r} _{G}} 、 r P / G {\displaystyle \mathbf {r} _{P/G}} 分别是点G的位置、点P对于点G的相对位置。

呈平移运动的刚体，其平移速度是矢量，是其位置矢量的时间变化率，即点G的速度。由于 r P / G {\displaystyle \mathbf {r} _{P/G}} 是常矢量，其时间变化率为零，点P的速度等于点G的速度：

同样原因，点P的加速度等于点G的加速度：

所以，呈平移运动的刚体，其内部所有质点的速度都相同、加速度也相同。

沙勒定理

当刚体移动时，它的位置与取向都可能会随着时间演进而改变。沙勒定理是欧拉旋转定律的一个推论。根据沙勒定理，刚体的最广义位移等价于一个平移加上一个旋转。所以，刚体运动可分为平移运动与旋转运动。刚体的现在位置与现在取向可以视为是从某个初始位置与初始取向经过平移与旋转而成。

挑选刚体内部一点G来代表整个刚体，从空间参考系S观测，点G的位置就是整个刚体在空间的位置，在刚体内部任意一点P的位置 r P {\displaystyle \mathbf {r} _{P}} 为

其中， r G {\displaystyle \mathbf {r} _{G}} 、 r P / G {\displaystyle \mathbf {r} _{P/G}} 分别是点G的位置、点P对于点G的相对位置。

刚体从时间 t 1 {\displaystyle t_{1}} 到时间 t 2 {\displaystyle t_{2}} 的运动，可以分为点G从 r G ( t 1 ) {\displaystyle \mathbf {r} _{G}(t_{1})} 到 r G ( t 2 ) {\displaystyle \mathbf {r} _{G}(t_{2})} 的平移运动，与位移 r P / G {\displaystyle \mathbf {r} _{P/G}} 从时间 t 1 {\displaystyle t_{1}} 到时间 t 2 {\displaystyle t_{2}} 的旋转运动。

点P的速度 v P {\displaystyle \mathbf {v} _{P}} 为

其中， v G {\displaystyle \mathbf {v} _{G}} 、 v P / G {\displaystyle \mathbf {v} _{P/G}} 分别是点G的速度、点P对于点G的相对速度。

点P的加速度 a P {\displaystyle \mathbf {a} _{P}} 为

其中， a G {\displaystyle \mathbf {a} _{G}} 、 a P / G {\displaystyle \mathbf {a} _{P/G}} 分别是点G的加速度、点P对于点G的相对加速度。

参阅

匀速运动

平抛运动

曲线运动

简谐运动

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。