性质

特殊酉群 SU(n) 是一个 n-1 维实矩阵李群。在拓扑上是紧及单连通的。在代数上，它是一个单李群（意为它的李代数是单的，见下）。SU(n) 的中心同构于循环群Zn。当 n ≥ 3，它的外自同构群是 Z2，而 SU(2) 的外自同构群是平凡群。

SU(n) 代数由 n 个算子生成，满换关系（对 i, j, k, l = 1, 2, ..., n）：

另外，算子

满足

这意味着 SU(n) 独立的生成元个数是 n-1。

生成元

一般地，SU(n) 的无穷小生成元 T，由一个无迹埃尔米特矩阵表示。即

以及

基本表示

在定义或基本表示中，由 n×n 矩阵表示的生成元是：

从而

我们也有

作为一个正规化约定。

伴随表示

在伴随表示中，生成元表示由 ( n 2 − − --> 1 ) × × --> ( n 2 − − --> 1 ) {\displaystyle (n^{2}-1)\times (n^{2}-1)} 矩阵表示，其元素由结构常数定义：

SU(2)

SU 2 ⁡ ⁡ --> ( C ) {\displaystyle \operatorname {SU} _{2}(\mathbb {C} )} 一个一般矩阵元素形如

这里 α α --> , β β --> ∈ ∈ --> C {\displaystyle \alpha ,\beta \in \mathbb {C} } 使得 | α α --> | 2 + | β β --> | 2 = 1 {\displaystyle |\alpha |^{2}+|\beta |^{2}=1} 。我们考虑如下映射 φ φ --> : C 2 → → --> M ⁡ ⁡ --> ( 2 , C ) {\displaystyle \varphi :\mathbb {C} ^{2}\to \operatorname {M} (2,\mathbb {C} )} ，（这里 M ⁡ ⁡ --> ( 2 , C ) {\displaystyle \operatorname {M} (2,\mathbb {C} )} 表示 2×2 复矩阵集合），定义为

考虑到 C 2 {\displaystyle \mathbb {C} ^{2}} 微分同胚于 R 4 {\displaystyle \mathbb {R} ^{4}} 和 M ⁡ ⁡ --> ( 2 , C ) {\displaystyle \operatorname {M} (2,\mathbb {C} )} 同胚于 R 8 {\displaystyle \mathbb {R} ^{8}} ，我们可看到 φ φ --> {\displaystyle \varphi } 是一个实线性单射，从而是一个嵌入。现在考虑 φ φ --> {\displaystyle \varphi } 限制在三维球面上，记作 S 3 {\displaystyle S^{3}} ，我们可发现这是三维球面到 M ⁡ ⁡ --> ( 2 , C ) {\displaystyle \operatorname {M} (2,\mathbb {C} )} 的一个紧子流形的一个嵌入。但显然有 φ φ --> ( S 3 ) = SU 2 ⁡ ⁡ --> ( C ) {\displaystyle \varphi (S^{3})=\operatorname {SU} _{2}(\mathbb {C} )} ，作为一个流形微分同胚于 SU 2 ⁡ ⁡ --> ( C ) {\displaystyle \operatorname {SU} _{2}(\mathbb {C} )} ，使 SU 2 ⁡ ⁡ --> ( C ) {\displaystyle \operatorname {SU} _{2}李群mathbb {C} )} 成为一个紧连通李群。

现在考虑李代数 s u 2 ( C ) {\displaystyle {\mathfrak {su}}_{2}(\mathbb {C} )} ，一个一般元素形如

这里 x ∈ ∈ --> R {\displaystyle x\in \mathbb {R} } 以及 β β --> ∈ ∈ --> C {\displaystyle \beta \in \mathbb {C} } 。易验证这样形式的矩阵的迹是零并为反埃尔米特的。从而李代数由如下矩阵生成

易见它具有上面提到的一般元素的形式。它们满足关系 u 3 u 2 = − − --> u 2 u 3 = u 1 {\displaystyle u_{3}u_{2}=-u_{2}u_{3}=u_{1}} 和 u 2 u 1 = − − --> u 1 u 2 = u 3 {\displaystyle u_{2}u_{1}=-u_{1}u_{2}=u_{3}} 。从而交换子括号由

确定。上述生成元与泡利矩阵有关， u 1 = i σ σ --> 1 {\displaystyle u_{1}=i\sigma _{1}} , u 2 = − − --> i σ σ --> 2 {\displaystyle u_{2}=-i\sigma _{2}} 及 u 3 = i σ σ --> 3 {\displaystyle u_{3}=i\sigma _{3}} 。

SU(3)

SU(3) 的生成元 T，在定义表示中为

这里 λ λ --> {\displaystyle \lambda \,} 为盖尔曼矩阵，是 SU(2) 泡利矩阵在 SU(3) 之类比：

注意它们都是无迹埃尔米特矩阵。

它们服从关系

d 的取值：

李代数

S U ( n ) {\displaystyle \mathrm {SU} (n)} 对应的李代数记作 s u ( n ) {\displaystyle {\mathfrak {su}}(n)} 。它的标准数学表示由无迹反埃尔米特 n × × --> n {\displaystyle n\times n} 复矩阵组成，以通常交换子为李括号物理学物理学家通常增加一个因子 i {\displaystyle i} ，从而所有矩阵成为埃尔米特的。这只不过是同一个实李代数一个不同的更方便的表示。注意 s u ( n ) {\displaystyle {\mathfrak {su}}(n)} 是 R {\displaystyle \mathbb {R} } 上一个李代数。

例如，下列量子力学中使用的矩阵组成 s u ( 2 ) {\displaystyle {\mathfrak {su}}(2)} 在 R {\displaystyle \mathbb {R} } 上的一组基：

（这里 i {\displaystyle i} 是虚数单位。）

这个表示经常用于量子力学（参见泡利矩阵以及盖尔曼矩阵）表示基本粒子比如电子的自旋。它们也作为我们三维空间量子相对论描述中的单位向量。

注意任意两个不同生成元的乘积是另一个生成元，以及生成元反交换。与单位矩阵（乘以 i {\displaystyle i} ）一起

它们也是 s u ( 2 ) {\displaystyle {\mathfrak {su}}(2)} 的生成元。

当然这里它取决于我们最终处理的问题，比如在非相对论量子力学中为 2-旋量；或在相对论狄拉克理论中，我们需要到 4-旋量的一个扩张；或在数学中甚至是克利福德代数。

注：在矩阵乘法下（在此情形是反交换的），生成克利福德代数 C l 3 {\displaystyle \mathrm {Cl} _{3}} ，而在交换子括号下生成李代数 s u ( 2 ) {\displaystyle {\mathfrak {su}}(2)} 。

回到一般的 S U ( n ) {\displaystyle \mathrm {SU} (n)} ：

如果我们选择（任意）一个特定的基，则纯虚数无迹对角 n × × --> n {\displaystyle n\times n} 矩阵子空间组成一个 n − − --> 1 {\displaystyle n-1} 维嘉当子代数。

将这个李代数复化，从而现在允许任何无迹 n × × --> n {\displaystyle n\times n} 矩阵。权本征向量是嘉当子代数自己，只有一个非零元素的矩阵不是对角的。尽管嘉当子代数 h {\displaystyle \mathrm {h} } 只是 n − − --> 1 {\displaystyle n-1} 维，但为了化简计算，经常引入一个辅助元素，与所有元素交换的单位矩阵（它不能视为这个李代数的一个元素）。故我们有一个基，其中第 i {\displaystyle i} 个基向量是在第 i {\displaystyle i} 个对角元素为 1 {\displaystyle 1} 而在其它处为零的矩阵。则权由 n {\displaystyle n} 个坐标给出，而且在所有 n {\displaystyle n} 个坐标求和为零（因为单位矩阵只是辅助的）。

故 S U ( n ) {\displaystyle \mathrm {SU} (n)} 的秩是 n − − --> 1 {\displaystyle n-1} ，它的邓肯图由 A n − − --> 1 {\displaystyle A_{n-1}} 给出，有 n − − --> 1 {\displaystyle n-1} 个顶点的链。

它的根系由 n ( n − − --> 1 ) {\displaystyle n(n-1)} 个根组成，生成一个 n − − --> 1 {\displaystyle n-1} 欧几里得空间。这里，我们使用 n {\displaystyle n} 冗余坐标而不是 n − − --> 1 {\displaystyle n-1} 对称标来强调根系的对称（ n {\displaystyle n} 坐标之和为零）。换句话说，我们是将这个 n − − --> 1 {\displaystyle n-1} 维向量空间嵌入 n {\displaystyle n} -维中。则根由所有 n ( n − − --> 1 ) {\displaystyle n(n-1)} 置换 ( 1 , − − --> 1 , 0 , … … --> , 0 ) {\displaystyle (1,-1,0,\dots ,0)} 。两段以前的构造解释了为什么。单根的一个选取为

它的嘉当矩阵是

它的外尔群或考克斯特群是对称群 S n {\displaystyle S_{n}} ， ( n − − --> 1 ) {\displaystyle (n-1)} -单形的对称群。

广义特殊酉群

对一个域 F，F 上广义特殊酉群 SU(p,q;F)，F 上一个秩为 n=p+q 的向量空间上使得一个符号为 (p,q) 的非退化埃尔米特形式不变的所有行列式为 1线性变换组成的群。这个酉群经常称为 F 上符号为 (p,q) 的特殊酉群。域 F 可以换为一个交换环，在这种情形向量空间换为自由模。

特别地，固定 GL(n,R) 中一个符号为 (p,q) 的埃尔米特矩阵，则所有

满足

经常可以见到记号 S U p , q {\displaystyle SU_{p,q}} 略去环或域，在这种形式环或域是指 C，这给出一个典型李群。当 F=C 时，A 的标准选取是

对某些维数 A 可能有更好的选择，当限制为 C 的一个子环时有更好表现。

例子

这类群的一个重要例子是皮卡模群 SU(2,1;Z[i])，（射影地）作用在二度复双曲空间上，同样地 SL(2,Z) （射影地）作用在二维实双曲空间上。2003年，Gábor Francsics 与彼得·拉克斯算出了这个群在 H C 2 {\displaystyle HC^{2}} 上作用的基本域，参见[1]。

另一个例子是 SU(1,1;C)，同构于 SL(2,R)。

重要子群

在物理学中，特殊酉群用于表示波色对称。在对称性破缺理论中寻找特殊酉群的子群很重要。在大一统理论中 SU(n) 重要的子群是，对 p>1，n-p>1：

为了完整性，还有正交与辛子群：

因为 SU(n) 的秩是 n-1，U(1) 是 1，一个有用的检验是看子群的秩是小于还是等于原来群的秩。SU(n) 是多个其它李群的子群：

有同构 SU(4)=Spin(6)，SU(2)=Spin(3)=USp(2) 以及 U(1)=Spin(2)=SO(2)。

最后值得指出的是 SU(2) 是 SO(3) 的二重覆叠群，这个关系在非相对论量子力学2-旋量的旋转中起着重要的作用。

相关条目

SU(2)的表示论

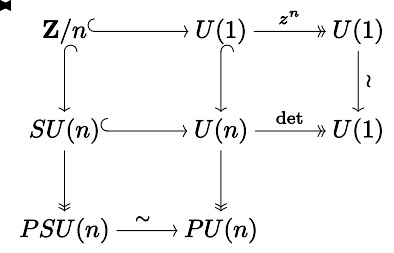
射影特殊酉群 PSU(n)

参考文献

Halzen, Francis; Martin, Alan. Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. 1984. ISBN 0-471-88741-2. 

Maximal Subgroups of Compact Lie Groups

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。