绝热压缩与绝热膨胀

绝热压缩与绝热膨胀通常由气体压强的变化引起。

绝热压缩发生在气压上升时，这时气体温度也会上升。例如，给自行车打气时，可以感觉到气筒温度上升，这正是因为气体压强上升的足够快到可视为绝热过程的缘故，热量没有逃逸，因而温度上升。柴油机在压缩冲程时正是靠绝热压缩原理来给燃烧室内的混合气体点火的。

绝热膨胀发生在气压下降时，这时气体温度也会下降。例如，给轮胎放气时，可以明显感觉到放出的气体比较凉，这正是因为气体压强下降的足够快到可视为绝热过程的缘故，气体内能转化为机械能，温度下降。

这些温度的变化量可以用理想气体状态方程精确计算。

用理想气体状态方程求解绝热过程

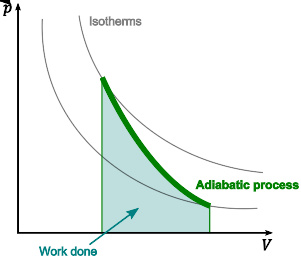
如图所示，在绝热膨胀过程（绿色粗线所示）中，气体的内能因转化为机械能做功（蓝色部分）而减少

对于经典气体（非费米气体、玻色气体）的方程如下，是一个多方方程：

其中：

对于绝热过程有：

C为常数，也可以写作：

绝热过程的热力学第一定律

绝热过程的热力学第一定律具体形式如下：

公式右边表示绝热过程气体对外做功。其中， N , R , γ γ --> {\displaystyle N,R,\gamma } 分别是该气体的物质的量、普适气体常数和绝热指数。

连续系统的解法

因为绝热过程没有热交换，所以 δ δ --> Q = 0 {\displaystyle \delta Q=0} ，由热力学第一定律，有

dU 为系统内能的变化量；δW是系统所做的功，做功必须耗费内能。由于δQ为零，可以得到

理想气体的内能可以由如下式子得到：

R 为理想气体常数；n为系统粒子的物质的量（因为绝热过程无粒子交换，所以恒定不变）； α α --> = f 2 {\displaystyle \alpha ={\frac {f}{2}}} 。

对（3）式两边微分，代入理想气体状态方程得到

因为 C V = α α --> R {\displaystyle C_{V}=\alpha R} ，（4）式通常写作 d U = n C V d T {\displaystyle dU=nC_{V}\,dT}

将（2）（3）（4）代入到（1），有：

简化得到：

两边同除以 PV

分别对 P 、 V 积分，得到

两边分别取幂：

消去负号：

因此得到：

和

Const为常数。

离散系统的解法

从状态1到状态2，系统的内能变化为：

同时，气体做功为：

因为绝热，所以有：

将（1）（2）式分别带入得到：

或：

因为实际情形下，通常可以假定气体质量数不变，该式可以简化为：

等熵线图

等熵线又称绝热线，是指P-V图中等熵的一条曲线，如右图黑色线条所示。等熵线有以下性质：

像等温线一样对称的趋近V轴与P轴。

每条等熵线只穿过同一条等温线一次。

等熵线与等温线相似，但斜率更大。

若等温线凹向45度方向处，则等熵线凹向31度方向处。

P-V图上一系列的等温—等熵线所绘出的眼形方块显示出向原点方向移动的趋势。参见能斯特定理。

下图是绝热线和等温线叠加的一个P-V图：

参见

绝热膨胀

绝热压缩

热力学

参考文献

汪志诚. 《热力学与统计物理（第三版）》. 高等教育出版社. 2003年3月.

吴大猷. 《热力学、气体运动论及统计物理》. 科学出版社. 1983年7月.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。