更多文章
更多精彩文章

相对补集
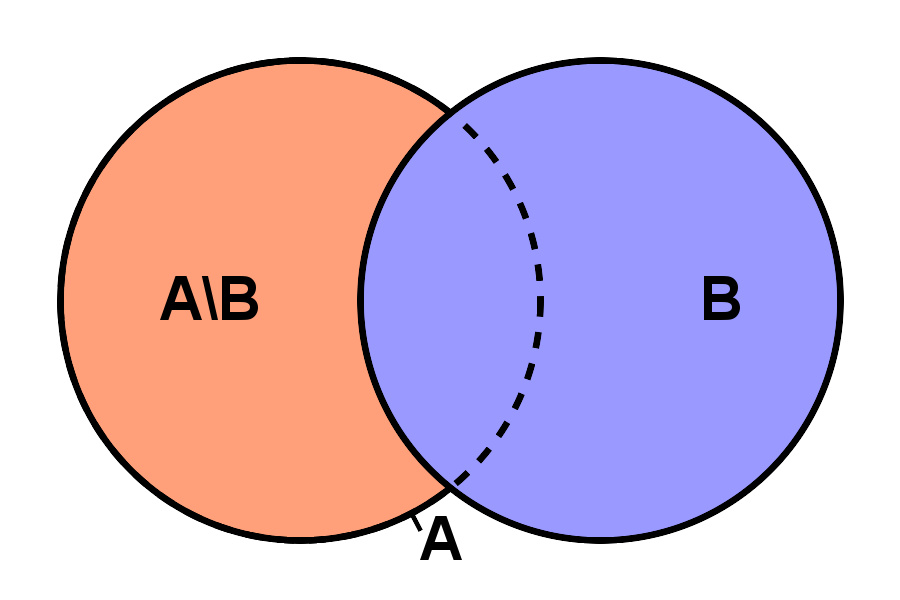
相对补集 A - B
若 A 和 B 是集合,则 A 在 B 中的 相对补集 ,是由所有属于 B 但不属于 A 的元素组成的集合。
A 在 B 中的相对补集通常写作 B − A (或 B \ A )。
形式上:
例如:
下列命题给出一些相对补集同并集和交集等集合论运算相关的一些常用性质。
命题1 :若 A , B , C 是集合,则下列等式恒成立:
绝对补集
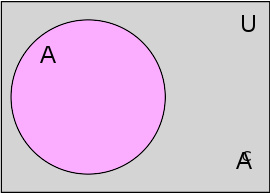
绝对补集
若给定 全集 U ,则 A 在 U 中的相对补集称为 A 的 绝对补集 (或简称 补集 ),写作 A ,即:
(注意:根据ISO与国家标准, A {\displaystyle A} 中子集 B {\displaystyle B} 的补集记作 ∁ ∁ --> A B {\displaystyle \complement _{A}B} 。)
例如,若全集为自然数集合,则奇数集合的补集为偶数集合。
下列命题给出一些绝对补集同并集和交集等集合论运算相关的一些重要性质。
命题2 :若 A 和 B 是全集 U 的子集,则下列恒等式成立:
上述表明,若 A 为 U 的非空子集,则{ A , A }是 U 的一个分割。
补集的符号
补集的符号为“ ∁ ”(Unicode:U+2201)。
参考
集合代数
朴素集合论
对称差
布尔逻辑
交集
并集
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。












{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}