二叉搜索树的查找算法

在二叉搜索树b中查找x的过程为：

若b是空树，则搜索失败，否则：

若x等于b的根节点的数据域之值，则查找成功；否则：

若x小于b的根节点的数据域之值，则搜索左子树；否则：

查找右子树。

/* 以下代码为C++写成，下同*/StatusSearchBST(BiTreeT,KeyTypekey,BiTreef,BiTree&p){//在根指针T所指二元查找樹中递归地查找其關键字等於key的數據元素，若查找成功，//則指针p指向該數據元素節點，并返回TRUE，否則指针指向查找路徑上訪問的最後//一個節點并返回FALSE，指针f指向T的雙親，其初始调用值為NULLif(!T){//查找不成功p=f;returnfalse;}elseif(key==T->data.key){//查找成功p=T;returntrue;}elseif(keydata.key)//在左子樹中繼續查找returnSearchBST(T->lchild,key,T,p);else//在右子樹中繼續查找returnSearchBST(T->rchild,key,T,p);}

在二叉搜索树插入节点的算法

向一个二叉搜索树b中插入一个节点s的算法，过程为：

若b是空树，则将s所指结点作为根节点插入，否则：

若s->data等于b的根节点的数据域之值，则返回，否则：

若s->data小于b的根节点的数据域之值，则把s所指节点插入到左子树中，否则：

把s所指节点插入到右子树中。（新插入节点总是叶子节点）

/*当二元搜尋樹T中不存在关键字等于e.key的数据元素时，插入e并返回TRUE，否则返回FALSE*/StatusInsertBST(BiTree*T,ElemTypee){if(!T){s=newBiTNode;s->data=e;s->lchild=s->rchild=NULL;T=s;//被插節点*s为新的根结点}elseif(e.key==T->data.key)returnfalse;//关键字等于e.key的数据元素，返回錯誤if(e.keydata.key)InsertBST(T->lchild,e);//將e插入左子樹elseInsertBST(T->rchild,e);//將e插入右子樹returntrue;}

在二叉查找树删除结点的算法

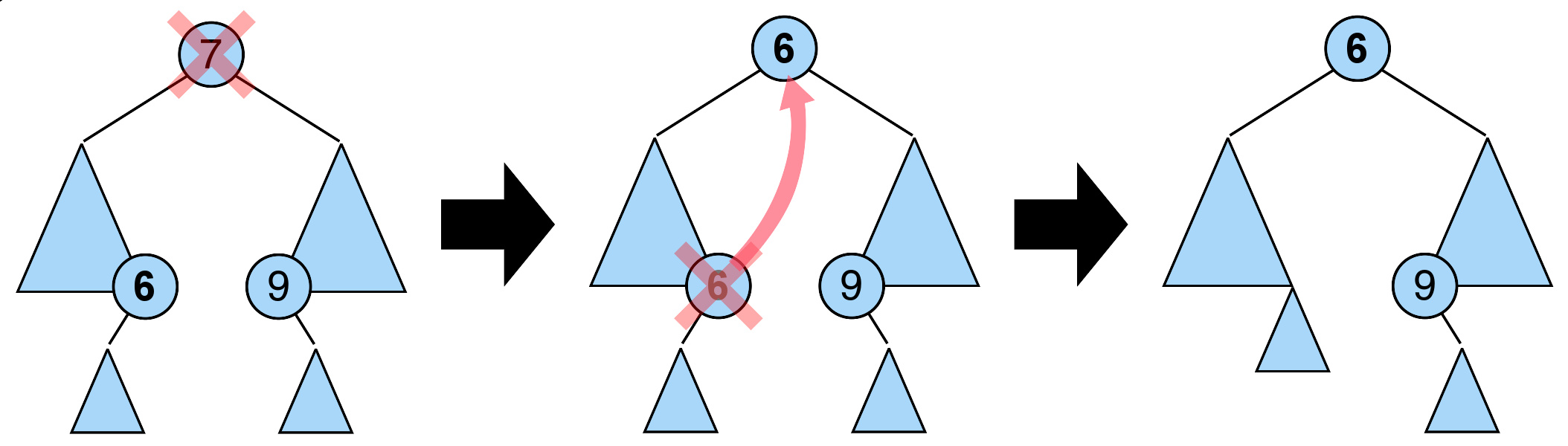
  删除一个有左、右子树的节点

在二叉查找树删去一个结点，分三种情况讨论：

若*p结点为叶子结点，即PL（左子树）和PR（右子树）均为空树。由于删去叶子结点不破坏整棵树的结构，则只需修改其双亲结点的指针即可。

若*p结点只有左子树PL或右子树PR，此时只要令PL或PR直接成为其双亲结点*f的左子树（当*p是左子树）或右子树（当*p是右子树）即可，作此修改也不破坏二叉查找树的特性。

若*p结点的左子树和右子树均不空。在删去*p之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整，可以有两种做法：其一是令*p的左子树为*f的左/右（依*p是*f的左子树还是右子树而定）子树，*s为*p左子树的最右下的结点，而*p的右子树为*s的右子树；其二是令*p的直接前驱（in-order predecessor）或直接后继（in-order successor）替代*p，然后再从二叉查找树中删去它的直接前驱（或直接后继）。

在二叉查找树上删除一个结点的算法如下：

StatusDeleteBST(BiTree*T,KeyTypekey){//若二叉查找树T中存在关键字等于key的数据元素时，则删除该数据元素，并返回//TRUE；否则返回FALSEif(!T)returnfalse;//不存在关键字等于key的数据元素else{if(key==T->data.key){// 找到关键字等于key的数据元素returnDelete(T);}elseif(keydata.key)returnDeleteBST(T->lchild,key);elsereturnDeleteBST(T->rchild,key);}}StatusDelete(BiTree*p){//该节点为叶子节点，直接删除BiTree*q,*s;if(!p->rchild&&!p->lchild){deletep;p=NULL;}elseif(!p->rchild){//右子树空则只需重接它的左子树q=p->lchild;p->data=p->lchild->data;p->lchild=p->lchild->lchild;p->rchild=p->lchild->rchild;deleteq;}elseif(!p->lchild){//左子树空只需重接它的右子树q=p->rchild;p->data=p->rchild->data;p->lchild=p->rchild->lchild;p->rchild=p->rchild->rchild;deleteq;}else{//左右子树均不空q=p;s=p->lchild;while(s->rchild){q=s;s=s->rchild;}//转左，然后向右到尽头p->data=s->data;//s指向被删结点的“前驱”if(q!=p)q->rchild=s->lchild;//重接*q的右子树elseq->lchild=s->lchild;//重接*q的左子树deletes;}returntrue;}

在C语言中有些编译器不支持为 struct Node 节点分配空间，声称这是一个不完全的结构，可使用一个指向该 Node 的指针为之分配空间。

如： sizeof( Probe ) ， Probe 作为二叉树节点在 typedef 中定义的指针。

Python实现：

deffind_min(self):# Gets minimum node (leftmost leaf) in a subtreecurrent_node=selfwhilecurrent_node.left_child:current_node=current_node.left_childreturncurrent_nodedefreplace_node_in_parent(self,new_value=None):ifself.parent:ifself==self.parent.left_child:self.parent.left_child=new_valueelse:self.parent.right_child=new_valueifnew_value:new_value.parent=self.parentdefbinary_tree_delete(self,key):ifkeyself.key:self.right_child.binary_tree_delete(key)else:# delete the key hereifself.left_childandself.right_child:# if both children are presentsuccessor=self.right_child.find_min()self.key=successor.keysuccessor.binary_tree_delete(successor.key)elifself.left_child:# if the node has only a *left* childself.replace_node_in_parent(self.left_child)elifself.right_child:# if the node has only a *right* childself.replace_node_in_parent(self.right_child)else:# this node has no childrenself.replace_node_in_parent(None)

二叉查找树的遍历

中序遍历（in-order traversal）二叉查找树的Python代码：

deftraverse_binary_tree(node,callback):ifnodeisNone:returntraverse_binary_tree(node.leftChild,callback)callback(node.value)traverse_binary_tree(node.rightChild,callback)

排序（或称构造）一棵二叉查找树

用一组数值建造一棵二叉查找树的同时，也把这组数值进行了排序。其最差时间复杂度为 O ( n 2 ) {\displaystyle O(n^{2})} 。例如，若该组数值经是有序的（从小到大），则建造出来的二叉查找树的所有节点，都没有左子树。自平衡二叉查找树可以克服上述缺点，其时间复杂度为O( n log n )。一方面，树排序的问题使得CPU Cache性能较差，特别是当节点是动态内存分配时。而堆排序的CPU Cache性能较好。另一方面，树排序是最优的增量排序（incremental sorting）算法，保持一个数值序列的有序性。

defbuild_binary_tree(values):tree=Noneforvinvalues:tree=binary_tree_insert(tree,v)returntreedefget_inorder_traversal(root):""" Returns a list containing all the values in the tree, starting at *root*. Traverses the tree in-order(leftChild, root, rightChild). """result=[]traverse_binary_tree(root,lambdaelement:result.append(element))returnresult

二叉查找树性能分析

每个结点的 C i {\displaystyle C_{i}} 为该结点的层次数。最坏情况下，当先后插入的关键字有序时，构成的二叉查找树蜕变为单支树，树的深度为 n {\displaystyle n} ，其平均查找长度为 n + 1 2 {\displaystyle {\frac {n+1}{2}}} （和顺序查找相同），最好的情况是二叉查找树的形态和折半查找的判定树相同，其平均查找长度和 log 2 ⁡ ⁡ --> ( n ) {\displaystyle \log _{2}(n)} 成正比（ O ( log 2 ⁡ ⁡ --> ( n ) ) {\displaystyle O(\log _{2}(n))} ）。

二叉查找树的优化

请参见主条目平衡树。

Size Balanced Tree(SBT)

加衡树(WBT)

AVL树

红黑树

Treap(Tree+Heap)

这些均可以使查找树的高度为 O ( log ⁡ ⁡ --> ( n ) ) {\displaystyle O(\log(n))}

参见

跳跃列表

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。