记法

V n {\displaystyle {\boldsymbol {V}}^{n}} ：维数为 n 的内积空间

v ∈ ∈ --> V n {\displaystyle {\boldsymbol {v}}\in {\boldsymbol {V}}^{n}} ： V n {\displaystyle {\boldsymbol {V}}^{n}} 中的元素，可以是向量、函数，等等

⟨ ⟨ --> v 1 , v 2 ⟩ ⟩ --> {\displaystyle \langle {\boldsymbol {v}}_{1},{\boldsymbol {v}}_{2}\rangle } ： v 1 {\displaystyle {\boldsymbol {v}}_{1}} 与 v 2 {\displaystyle {\boldsymbol {v}}_{2}} 的内积

s p a n { v 1 , v 2 , … … --> , v n } {\displaystyle \mathrm {span} \{{\boldsymbol {v}}_{1},{\boldsymbol {v}}_{2},\ldots ,{\boldsymbol {v}}_{n}\}} ： v 1 {\displaystyle {\boldsymbol {v}}_{1}} 、 v 2 {\displaystyle {\boldsymbol {v}}_{2}} …… v n {\displaystyle {\boldsymbol {v}}_{n}} 张成的子空间

p r o j v u = ⟨ ⟨ --> u , v ⟩ ⟩ --> ⟨ ⟨ --> v , v ⟩ ⟩ --> v {\displaystyle \mathrm {proj} _{\boldsymbol {v}}\,{\boldsymbol {u}}={\langle {\boldsymbol {u}},{\boldsymbol {v}}\rangle \over \langle {\boldsymbol {v}},{\boldsymbol {v}}\rangle }{\boldsymbol {v}}} ： u {\displaystyle {\boldsymbol {u}}} 在 v {\displaystyle {\boldsymbol {v}}} 上的投影

基本思想

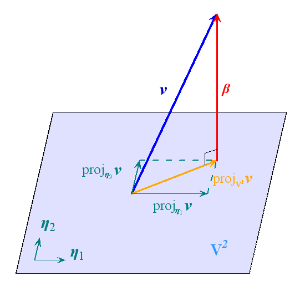
图1 v {\displaystyle {\boldsymbol {v}}} 在 V 2 {\displaystyle {\boldsymbol {V}}^{2}} 上投影，构造 V 3 {\displaystyle {\boldsymbol {V}}^{3}} 上的正交基 β β --> {\displaystyle {\boldsymbol {\beta }}}

Gram-Schmidt正交化的基本想法，是利用投影原理在已有正交基的基础上构造一个新的正交基。

设 v ∈ ∈ --> V n {\displaystyle {\boldsymbol {v}}\in {\boldsymbol {V^{n}}}} 。 V k {\displaystyle {\boldsymbol {V}}^{k}} 是 V n {\displaystyle {\boldsymbol {V}}^{n}} 上的 k {\displaystyle k} 维子空间，其标准正交基为 { η η --> 1 , … … --> , η η --> k } {\displaystyle \{{\boldsymbol {\eta }}_{1},\ldots ,{\boldsymbol {\eta }}_{k}\}} ，且 v {\displaystyle {\boldsymbol {v}}} 不在 V k {\displaystyle {\boldsymbol {V}}^{k}} 上。由投影原理知， v {\displaystyle {\boldsymbol {v}}} 与其在 V k {\displaystyle {\boldsymbol {V}}^{k}} 上的投影 p r o j V k v {\displaystyle \mathrm {proj} _{\boldsymbol {V^{k}}}{\boldsymbol {v}}} 之差

是正交于子空间 V k {\displaystyle {\boldsymbol {V}}^{k}} 的，亦即 β β --> {\displaystyle {\boldsymbol {\beta }}} 正交于 V k {\displaystyle {\boldsymbol {V}}^{k}} 的正交基 η η --> i {\displaystyle {\boldsymbol {\eta }}_{i}} 。因此只要将 β β --> {\displaystyle {\boldsymbol {\beta }}} 单位化，即

那么 { η η --> 1 , … … --> , η η --> k , η η --> k + 1 } {\displaystyle \{{\boldsymbol {\eta }}_{1},\ldots ,{\boldsymbol {\eta }}_{k},{\boldsymbol {\eta }}_{k+1}\}} 就是 V k {\displaystyle {\boldsymbol {V}}^{k}} 在 v {\displaystyle {\boldsymbol {v}}} 上扩展的子空间 s p a n { v , η η --> 1 , . . . , η η --> k } {\displaystyle \mathrm {span} \{{\boldsymbol {v}},{\boldsymbol {\eta }}_{1},...,{\boldsymbol {\eta }}_{k}\}} 的标准正交基。

根据上述分析，对于向量组 { v 1 , … … --> , v m } {\displaystyle \{{\boldsymbol {v}}_{1},\ldots ,{\boldsymbol {v}}_{m}\}} 张成的空间 V m {\displaystyle {\boldsymbol {V}}^{m}} ( m < n {\displaystyle m )，只要从其中一个向量（不妨设为 v 1 {\displaystyle {\boldsymbol {v}}_{1}} ）所张成的一维子空间 s p a n { v 1 } {\displaystyle \mathrm {span} \{{\boldsymbol {v}}_{1}\}} 开始（注意到 v 1 {\displaystyle {\boldsymbol {v}}_{1}} 就是 s p a n { v 1 } {\displaystyle \mathrm {span} \{{\boldsymbol {v}}_{1}\}} 的正交基），重复上述扩展构造正交基的过程，就能够得到 V n {\displaystyle {\boldsymbol {V}}^{n}} 的一组正交基。这就是 Gram-Schmidt正交化 。

算法

首先需要确定已有基底向量的顺序，不妨设为 { v 1 , … … --> , v n } {\displaystyle \{{\boldsymbol {v}}_{1},\ldots ,{\boldsymbol {v}}_{n}\}} 。Gram-Schmidt正交化的过程如下：

这样就得到 s p a n { v 1 , … … --> , v n } {\displaystyle \mathrm {span} \{{\boldsymbol {v}}_{1},\ldots ,{\boldsymbol {v}}_{n}\}} 上的一组正交基 { β β --> 1 , … … --> , β β --> n } {\displaystyle \{{\boldsymbol {\beta }}_{1},\ldots ,{\boldsymbol {\beta }}_{n}\}} ，以及相应的标准正交基 { η η --> 1 , … … --> , η η --> n } {\displaystyle \{{\boldsymbol {\eta }}_{1},\ldots ,{\boldsymbol {\eta }}_{n}\}} 。

考察如下欧几里得空间 R 中向量的集合，欧氏空间上内积的定义为 = b a ：

下面作Gram－Schmidt正交化，以得到一组正交向量：

下面验证向量 β β --> 1 {\displaystyle {\boldsymbol {\beta }}_{1}} 与 β β --> 2 {\displaystyle {\boldsymbol {\beta }}_{2}} 的正交性：

将这些向量单位化：

于是 { η η --> 1 , η η --> 2 } {\displaystyle \{{\boldsymbol {\eta }}_{1},{\boldsymbol {\eta }}_{2}\}} 就是 s p a n { v 1 , v 2 } {\displaystyle \mathrm {span} \{{\boldsymbol {v}}_{1},{\boldsymbol {v}}_{2}\}} 的一组标准正交基底。

不同的形式

随着内积空间上内积的定义以及构成内积空间的元素的不同，Gram-Schmidt正交化也表现出不同的形式。

例如，在实向量空间上，内积定义为：

在复向量空间上，内积定义为：

函数之间的内积则定义为：

与之对应，相应的Gram－Schmidt正交化就具有不同的形式。

参见

内积空间

内积

正交

QR分解

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。