豪斯霍尔德变换
定义
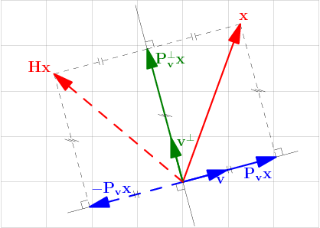
豪斯霍尔德变换示意图:向量x在豪斯霍尔德向量v的超平面v⊥ ⊥ -->{\displaystyle \mathbf {v} ^{\perp }}上的镜像是Hx,H是豪斯霍尔德矩阵。
如果 v{\displaystyle v} 给出为单位向量而 I{\displaystyle I} 是单位矩阵,则描述上述线性变换的是 豪斯霍尔德矩阵 (v∗ ∗ -->{\displaystyle v^{*}} 表示向量 v{\displaystyle v} 的共轭转置)
性质
豪斯霍尔德矩阵有如下性质:
它是埃尔米特矩阵:H=H∗ ∗ -->{\displaystyle H=H^{*}\,}
它是正交矩阵:H− − -->1=H∗ ∗ -->{\displaystyle H^{-1}=H^{*}\,}
因此也是对合的:H2=I{\displaystyle H^{2}=I\,}.
进一步的,H{\displaystyle H} 实际上按上面描述的那样反射了点X{\displaystyle X} (用它的位置向量x{\displaystyle x} 来识别),因为
这里的 ⟨ ⟨ -->,⟩ ⟩ -->{\displaystyle \langle ,\rangle } 表示点积。注意 ⟨ ⟨ -->v,x⟩ ⟩ -->{\displaystyle \langle v,x\rangle } 等于从 X 到超平面的距离。
应用
豪斯霍尔德变换可以将向量的某些元素置零,同时保持该向量的范数不变。例如,将非零列向量x=[x1,… … -->,xn]T{\displaystyle \mathbf {x} =[x_{1},\ldots ,x_{n}]^{T}}变换为单位基向量e=[1,0,… … -->,0]T{\displaystyle \mathbf {e} =[1,0,\ldots ,0]^{T}}的豪斯霍尔德矩阵为
其中豪斯霍尔德向量v{\displaystyle \mathbf {v} }满足:
Dubrulle 在2000年给出了将豪斯霍尔德变换应用于生成一个一般的稀疏向量的一个数值稳定的算法。
对一个矩阵的各个列向量逐一进行相应的豪斯霍尔德变换,可以将这个矩阵变换为上海森伯格矩阵、上三角矩阵等形式。后者就是QR分解的豪斯霍尔德算法。
参见
线性变换
数值计算
Givens旋转
QR分解
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








24小时热门
推荐阅读

知识互答
关于我们

APP下载
























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}