多面体的运算

下面列出康威多面体表示法中，多面体的运算符号，那些运算通常类似几何变换，并以 (v,e,f) 表示进行该运算或操作后多面体的变化。

这些运算符号的运算优先级皆为由右至左。例如：

正四面体的对偶多面体计为dT;

截角的正方体应计为t3C 或 tC;

截角的截半立方体应计为 t4aC 或 taC。

所有的操作都保有对称性，除了s和g是扭曲的像并失去了镜射对称。

例子

生成标准种子

所有的五个正多面体皆可以从棱柱种子经过零至两个运算或操作而产生：

锥体:Y3 (正四面体是一个特别的角锥)

反柱体:A3 (正八面体是一个特别的反柱体)

柱体:P4 (正方体是一个特别的柱体)

五角反棱柱: A5

康威的符号扩展

上述的运算和操作可以从正多面体种子或柱体锥体的种子产生所有的半正多面体、卡塔兰立体、柏拉图立体和阿基米德立体。 许多多面体都可由高阶的组合操作还表示，但是某些特别的多面体需要更多的符号来表示。

例如，几何艺术家George W. Hart定义他的操作称为"propellor"，和另一个反映创建镜像图像的旋转形式"reflect"。

p – "propellor" (旋转建立四边形于顶点). 这个操作的对偶多面体是本身: dpX=pdX.

r – "reflect" – 对种子进行镜射变换.一般没已影响，除非有s或g的种子

詹森多面体扩展

为了表达詹森多面体，诺曼·詹森也定义了一些符号来表达它的多面体

下列种子都必须要在后面加注边数:

扩展的符号:

例如:

其它的扩展

下面扩展符号也可以用于康威多面体表示法，但是在施莱夫利符号中，更为常用。

t0,1 = 截角

t0,2 = 截边:小斜方截半

t0,1,2 = 截边再截角:大斜方截半

t0,3 = 截面:向下锯齿(Runcination) : 切割多面体，同时沿面、边和顶点，建立新的面代替原来的面、边和顶点中心。

t0,1,3 = 截面再截角

t0,2,3 = 截面再截边

t0,1,2,3 = 截面再截边再截角

t0,4 = 截胞 : 切割多胞体，同时沿胞、面、边和顶点，建立新的胞代替原来的胞、面、边和顶点中心。

t1 = 截半

t1,2 = 截半再截边:双截角

t2

h = 交替 alternate

例如:

"hC" =正四面体

几何座标的衍生形式

密铺

几何体

其他多面体

迭代简单简单操作的形式，可以产生更大的多面体，并保持基本对称性。顶点被假设是对相同半径的球面。

四面体对称

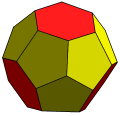
截角三角化四面体 "t6dtT"

八面体对称

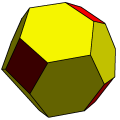
截角菱形十二面体 "t4daC"

四角化截半立方体 "k4aC"

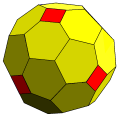
截角五角化二十四面体 "dk4sC"

二十面体对称

菱形

菱形九十面体 "dakD"

三角形

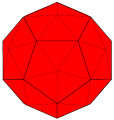
五角化十二面体 "kD"

五角化截半二十面体 "k5aD"

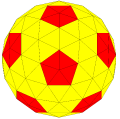
"k6k5tI"

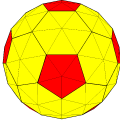
六角化五角化截角菱形三十面体 "kt5daD"

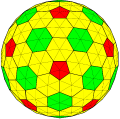
"kdktI" "dtktI"

"kdkt5daD"

对偶

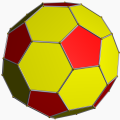
截角二十面体 "dkD"

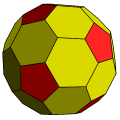
截角菱形三十面体 "t5daD" "cD"

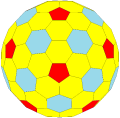
"dk6k5tI"

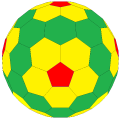
"dkt5daD"

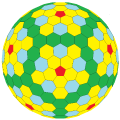
"tktI"

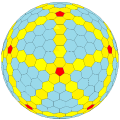
"tkt5daD"

手性

五角化六十面体 "dsD"

五角化扭棱十二面体 "k5sD"

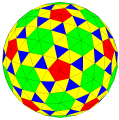
六角化五角化扭棱截角二十面体 "k5k6stI" "kdk5sD"

手性对偶

扭棱十二面体 "sD"

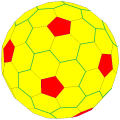
截角五角化六十面体 "dk5sD"

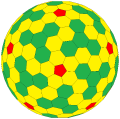
"dk5k6stI" "tk5sD"

参见

均匀多面体

图形算法

外部链接和参考文献

George Hart"s Conway interpreter: generates polyhedra inVRML, taking Conway notation as input

polyHédronisme: generates polyhedra in HTML5 canvas, taking Conway notation as input

MathWorld上Conway Polyhedron Notation的资料，作者：埃里克·韦斯坦因。

John Conway"s notation

MathWorld上Truncation的资料，作者：埃里克·韦斯坦因。 (truncate)

MathWorld上Rectification的资料，作者：埃里克·韦斯坦因。 (ambo)

MathWorld上Cumulation or Apiculation的资料，作者：埃里克·韦斯坦因。 (kis)

Conway operators, PolyGloss, Wendy Krieger

Derived Solids

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。