凸面镜

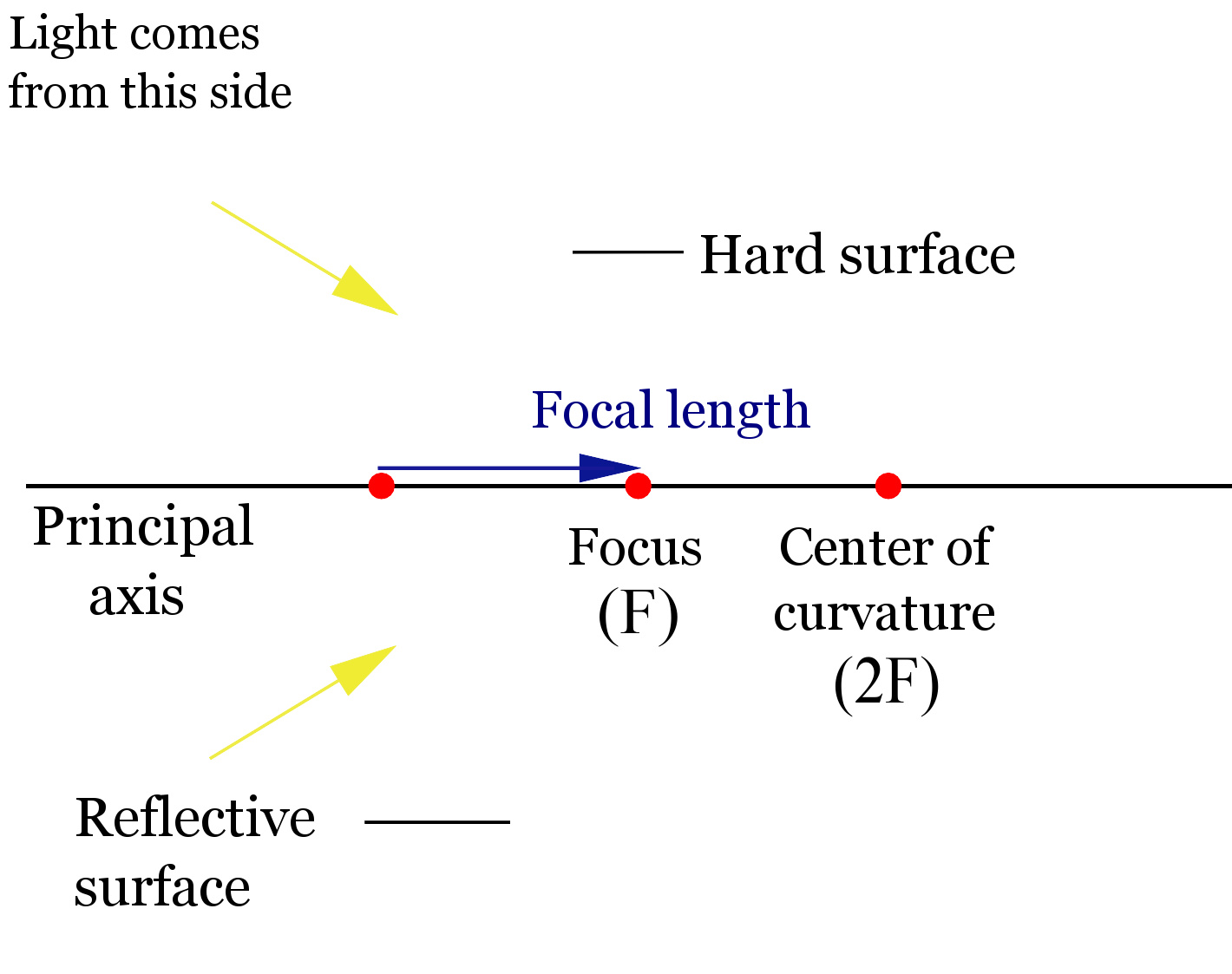
  一个凸面镜的图解，显示出焦点、焦距、曲率中心、主轴等等。

凸面镜或发散镜是将光线由表面朝向光源反射的曲面镜。这种镜子只能形成虚像，因为焦点F和曲率中心2F两者都是在镜面内侧，实际上并不存在的虚点。

准直（平行）的一束光线被凸面镜反射后会发散，因为镜子表面每个点的法线是不同方向的。

影像

影像永远是虚像（光线没有真正的穿过影像）、缩小的（较小）正像。这个特色使凸面镜非常有用：在镜子上的一切看起来都变小，所以可以将影像“压缩”，比平面镜涵盖更大的视场。在汽车上的乘客侧镜就是典型的凸面镜。在一些国家，这些镜子还需要标示安全警示：“实际的物体比所见的更为接近”，以提醒驾驶凸面镜的扭曲对距离判断所造成的影响。

光路图

凹面镜

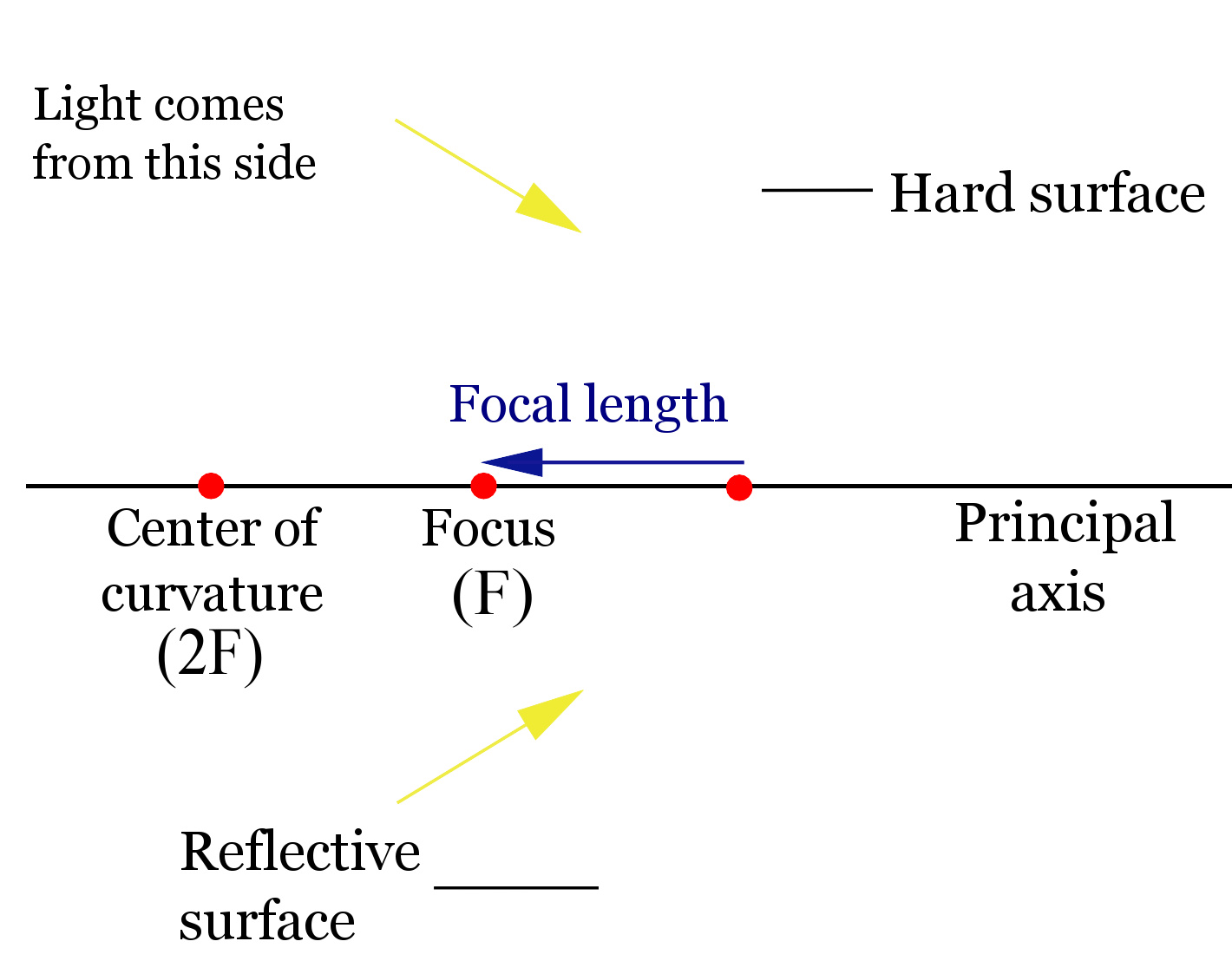
  一个凹面镜的图解，显示出焦点、焦距、曲率中心、主轴等等。

凹面镜或汇聚镜会将反射的光线像内偏折（永远朝像入射光源）。不同于凸面镜，凹面镜会因为物体与镜面本身距离的不同，而呈现不同的影像。

这种镜面称为"汇聚"，因为它们倾向将射至表面的光线收集起来，平行入射的光线将会被重新汇集在焦点上，这也是因为表面每个点的法线方向不同，光线以不同的角度反射。

影像

注：此处S表示物体与镜面的距离。

当 S < F {\displaystyle S ，影像是：

当 S = F {\displaystyle S=F} ，影像形成在无穷远处（∞）。

当 F < S < 2 F {\displaystyle F，影像是：

当 S = 2 F {\displaystyle S=2F} ，影像是：

当 S > 2 F {\displaystyle S>2F} ，影像是：

镜子的形状

多数的曲面镜都是球面的外观，因为这是最容易制作，也是最通用的形状。但是球面镜易产生球面像差，平行的光线反射后不能汇聚在单一的焦点上。平行的光线，例如来自非常遥远目标的光，使用抛物面镜可以获得更好的效果，因为抛物面镜汇聚的光点比球面镜的更小。

球面镜的数学论述

在数学的论述下，平轴近似，意味着以下的第一近似是将球面反射镜当成抛物面反射镜。一个球面的凹面反射镜的球面反射镜的光矩阵显示如下： C {\displaystyle C} 是矩阵的元素 − − --> 1 f {\displaystyle -{\frac {1}{f}}} ，此处 f {\displaystyle f} 是光学设计上的焦点。

方块1和方块3的特性是角度的和是π（180°），方块2显示Maclaurin系列第一阶的弧长为 arccos ⁡ ⁡ --> ( − − --> r R ) {\displaystyle \arccos \left(-{\frac {r}{R}}\right)} 。凸球面镜导出的光矩阵和薄透镜是非常相似的。

制镜方程式和放大率

制镜方程式是物距（ d o {\displaystyle d_{o}} ）和像距（ d i {\displaystyle d_{i}} ）到焦点（ f {\displaystyle f} ）距离的关系。

1 d o + 1 d i = 1 f {\displaystyle {\frac {1}{d_{o}}}+{\frac {1}{d_{i}}}={\frac {1}{f}}}

镜子的放大率是像距的高除以物距的高。

m = − − --> d i d o {\displaystyle m=-{\frac {d_{i}}{d_{o}}}}

在这里的负号只是一种惯例，只是单纯的放在此处。使用上面这个公式时，如果放大率是正值，影像是正立的；放大率是负值，影像是反转的（上下倒转）。

考虑一个凹面镜，曲率半径是30公分，一个10公分高的物体放在镜子前面18公分的距离上。一束来自顶端（在光轴上方10公分）射向镜心（光轴与镜面的交点，或是镜子的中心点）的光线将形成一个角度，被镜面反射时会在光轴的另一面以和入射角相同的角度反射，请记住：入射角等于反射角。

第二束光线可以从物体的顶端画向焦点并且会在光轴下方的镜子表面的某一个点被反射。依照规则，通过焦点的光线被反射时会平行于光轴。这两束反射光的交点，就是影像的顶点位置（成像的位置）。

影像的高度 h i {\displaystyle h_{i}} 和物体的高度 h o {\displaystyle h_{o}} 在大小上是不一样的，但是可以考虑由早先所提及的这两束光线所构成的直角三角形，同样的，物体的距离 d o {\displaystyle d_{o}} 和影像的距离 d i {\displaystyle d_{i}} 也是相似的。

h o h i = d o d i {\displaystyle {\frac {h_{o}}{h_{i}}}={\frac {d_{o}}{d_{i}}}}

这个等式可以重新写成在图中所提到的：

h o h i = d o − − --> f f {\displaystyle {\frac {h_{o}}{h_{i}}}={\frac {d_{o}-f}{f}}}

两边都除以 d o {\displaystyle d_{o}} ，并且重新改写就是制镜方程式：

1 d o + 1 d i = 1 f {\displaystyle {\frac {1}{d_{o}}}+{\frac {1}{d_{i}}}={\frac {1}{f}}}

参考资料

曲面镜光学原理

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。