定义

对于实数x，指数积分Ei(x)可以定义为：

其中et{\displaystyle e^{t}}为指数函数。以上的定义可以用于正数x，但这个积分必须用柯西主值的概念来理解。

对于自变量是复数的情形，这个定义就变得模棱两可了 。为了避免歧义，我们使用以下的记法：

当自变量的实数部分为正时，可以转换为：

Ei与E1有以下关系：

性质

收敛级数

指数积分可以用以下的收敛级数来表示：

其中 γ γ -->≈ ≈ -->0.5772156649015328606... {\displaystyle ~\gamma \approx 0.5772156649015328606欧拉.~}是欧拉-马歇罗尼常数。这个级数在自变量为任何复数时都是收敛的，但Ei的定义则需要 x>0 {\displaystyle ~x\!>\!0~}。

渐近（发散）级数

截断和中取 N {\displaystyle ~N~}项时，渐近展开式的相对误差

自变量的值较大时，用以上的收敛级数来计算指数积分是困难的。在这种情况下，我们可以使用发散（或渐近）级数：

这个截断和可以用来计算 Re(z)≫ ≫ -->1 {\displaystyle ~{\rm {Re}}(z)\!\gg \!1~}时函数的值。级数中的项数越多，自变量的实数部分就应该越大。

图中描述了以上估计的相对误差。

指数和对数的表现

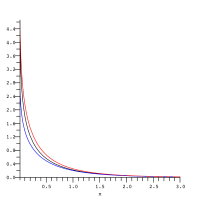
 E1 {\displaystyle ~E_{1}~}在自变量较大时的表现类似指数函数，自变量较小时类似对数函数。 E1 {\displaystyle ~E_{1}~}是位于以下两个函数之间的：

这个不等式的左端在图中用红色曲线来表示，中间的黑色曲线是 E1(x) {\displaystyle ~{\rm {E}}_{1}(x)~}，不等式的右端用蓝色曲线来表示。

与其它函数的关系

指数积分与对数积分li(x)有密切的关系：

另外一个有密切关系的函数，具有不同的积分限：

这个函数可以视为把指数积分延伸到负数：

我们可以把两个函数都用整函数来表示：

利用这个函数，我们可以用对数来定义：

以及

指数积分还可以推广为：

它是不完全伽玛函数的一个特例：

这个推广的形式有时成为Misra函数φ φ -->m(x){\displaystyle \varphi _{m}(x)}，定义为：

导数

函数 En {\displaystyle ~{\rm {E}}_{n}~}与 E1 {\displaystyle ~{\rm {E}}_{1}~}的导数有以下简单的关系：

然而，这里假设了 n {\displaystyle ~n~}是整数；复数 n {\displaystyle ~n~}的推广还没有在文献中报导，虽然这种推广是有可能的。

复变量指数积分

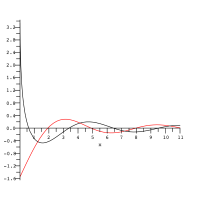
E1(i x){\displaystyle {\rm {E}}_{1}({\rm {i}}\!~x)} versus  x {\displaystyle ~x~}, real part(black) and imaginary part (red).

从以下的表示法中

可以看出指数积分与正弦积分（Si）和余弦积分（Ci）之间的关系：

图中的黑色和红色曲线分别描述了 E1(x) {\displaystyle ~{\rm {E}}_{1}(x)~}的实数和虚数部分。

参考文献

Press, William H. et al. Numerical Recipes (FORTRAN). Cambridge University Press, New York: 1989.

Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 5)

R. D. Misra, Proc. Cambridge Phil. Soc. 36, 173 (1940)

S. Chandrasekhar, Radiative transfer, reprinted 1960, Dover

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。