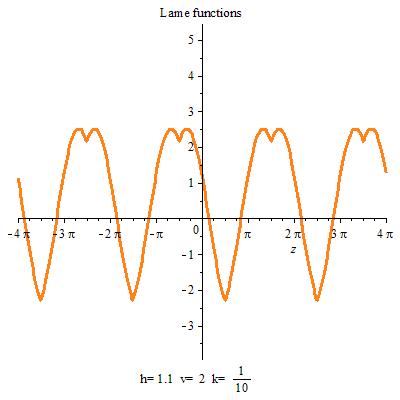
拉梅函数(Lame functions)是下列拉梅方程的解:
-
雅可比形式
d 2 w d z 2 + ( A + v ( v + 1 ) k 2 s n 2 ( z , k ) ) w = 0 {\displaystyle {\frac {d^{2}w}{dz^{2}}}+(A+v(v+1)k^{2}sn^{2}(z,k))w=0} 
+ 此拉梅方程的正则奇点在复数平面的 2 p K + ( 2 q + 1 ) ∗ i K ′ {\displaystyle 2pK+(2q+1)*iK"} 
其中 p,q ∈Z,K代表模数为k的完全椭圆积分，K"代表模数为 k ′ = 1 − k 2 {\displaystyle k"={\sqrt {1-k^{2}}}} 
的完全椭圆积分。
其中 k,v 都是实数，并且 0 < k < 1 {\displaystyle 0 
,
-
代数形式
作雅可比椭圆函数变数替换 s = s n 2 ( z , k ) {\displaystyle s=sn^{2}(z,k)} 
得拉梅方程的代数形式：
d 2 Λ d s 2 + 1 2 ∗ ( 1 2 + 1 s − 1 + 1 s − h ) ∗ d Λ d s − n ( n + 1 ) s + H 4 s ...
