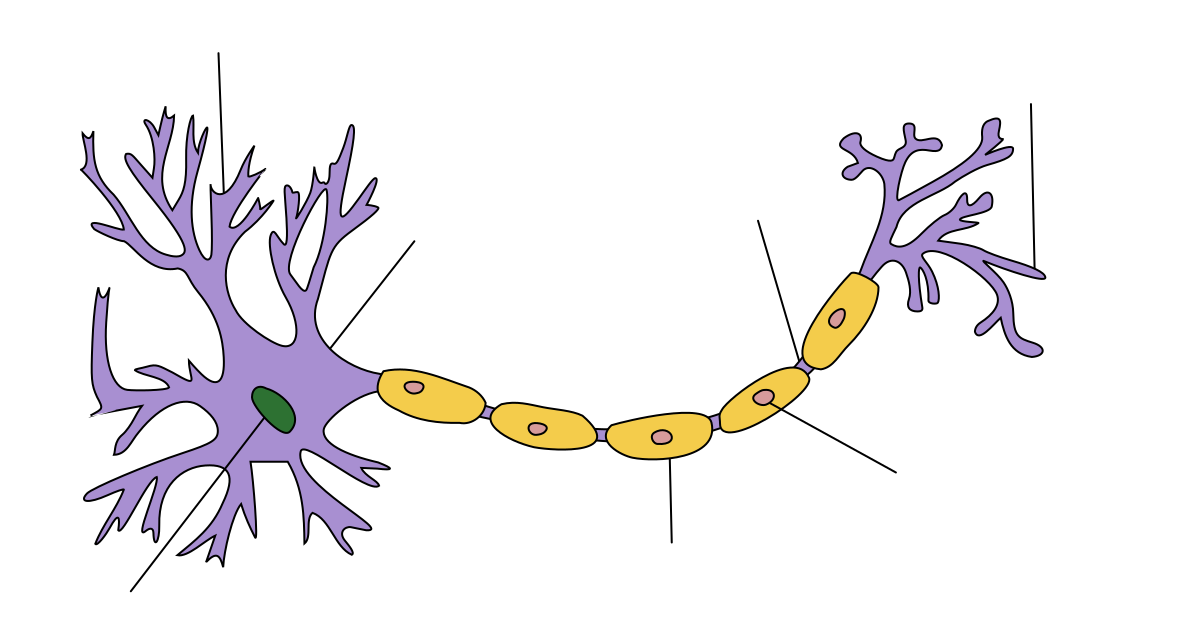
跳跃式传导(英语:saltatory conduction)是动作电位沿有髓鞘轴突由一个兰氏结传导到下一个兰氏结的过程,它能在不增加轴突直径的情况下增加动作电位的神经传导速度(nerve conduction velocity)。只有兰氏结能产生动作电位,该电位以跳跃的方式进行传导,一定长度的轴突内需产生动作电位的次数较少,所以有髓鞘轴突中动作电位传导的速度较无髓鞘轴突的传导快。“跳跃式传导”译自英文“saltatory conduction”,而其中的“saltatory”源于拉丁文“saltare”(意为“跳跃”)。