黄油猫悖论是一种把两个有明确结果的理论结合到一起去论证，就由一个神奇的结果，两个明确结果的理论总是背道而驰。有很多的实验围绕着黄油猫悖论来进行，但是却没有一个实验能够同时证明两个理论。

　　黄油猫悖论Buttered cat paradox，它主要是把两种民间常识共同组合而成的一种恶搞的悖论，因此该常识主要为猫在半空当中突然跳下来，而且它也只能永远的用脚去着陆。如果把黄油吐司高高的抛到半空当中，然而被抛到半空当中的吐司将永远都会在涂上黄油的那一面先行落地。因此这个悖论就出在，当你把黄油吐司没有涂上黄油的那一面黏着猫的背部之时。依照以上两条定律，猫根本就无法用脚着陆，因为黄油吐司将会永远在涂上黄油的那一面落地。但同样的，如果黄油吐司涂上黄油的那一面根本就无法落地，因为猫将会永远的用脚着陆。

　　黄油猫悖论，这个悖论主要是由两种民间的智慧组合而成的一种玩笑式的悖论，同样也是一个十分有趣的一种思想实验。我们暂时先确定有两条定律即猫将会永远用脚去着陆。黄油吐司将会永远在涂上黄油的那一面先行落地。都是一个千真万确的事和有证据可以用来证明的事。那么，如果把黄油吐司没有涂上黄油的那一面黏着猫的背部(下文简称黄油猫)之时，黄油猫究竟会发生什么样的反应呢?

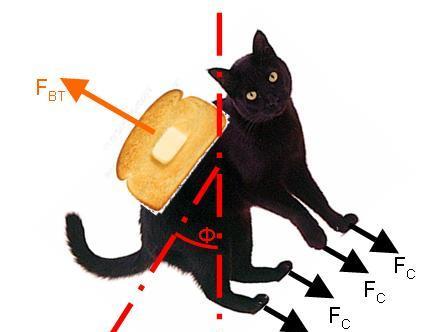
　　黄油猫悖论主要是因为某些人曾经打趣地表示，通过黄油猫的一个实验将会导致一个反地心引力的主要作用。他们也曾经猜测，如果黄油猫在半空当中落地之时，它将会渐渐的减速和不停的转动，在它最终到达一种恒稳状态时，将会与地面浮着一个十分短的距离并进行高速的转动，从而使得吐司没有涂上黄油的一面和猫背根本就无法接触到地面。

　　黄油猫悖论这种解释十分的诙谐有趣，如果我们可以假设两种定律都是十分正确的话，那么也极有可能什么事情都可能会发生。然而，如果依照以上两种解释，必须要有某一种能量可以维持黄油猫的一种恒稳状态，否则它将会违反这种能量的守恒定律。不过，亦有很多方法可以使黄油猫得到这种能量，例如在它转动时，黄油猫能在摩擦空气当中得出一些热量、或者从阳光，并让它直接转换成一种直接动能。虽然能够证明这一点是一件很艰苦的事，但是却并非完全不可能实现。

　　黄油猫悖论当中的其他实验结果就是，黄油猫用脚着陆，但又开始立即反转。然而这样的结果也就意味着黄油猫的脚远远要比吐司涂上黄油的那一面对地心引力更具有吸引力，但是同一实验，吐司涂上黄油的那一面也曾经击败过黄油猫脚。这直接取决于最初的那个实验开始的主要参量，到底是黄油猫的脚或者是吐司涂上黄油的那一面对地心引力更具有吸引力?当然两者都是相当正确的，因为另一种实验结果就是，让吐司首先着地，这也就意味着黄油猫实际上并未登陆在地上，因为吐司照样在黄油猫的背面，然后黄油猫用脚去打滚。

　　黄油猫悖论是在2003年的6月，金伯利•米那以影片《永久行动》同时也为她赢取了一个学生学院奖。由于金伯利的影片也是根据她的一个高中朋友的一篇探索黄油猫悖论的一些潜在涵义的论文所进行拍摄的。如果依照以上的两条定律，那么黄油猫根本就无法用脚着陆，因为黄油吐司将会永远在涂上黄油的那一面落地。但是同样的，黄油吐司所涂上黄油的那一面根本就无法落地，因为黄油猫将会永远去用脚着陆。科学神奇地解释了这个永动机所存在的极大可能性。

　　黄油猫悖论主要是凭着直觉猜一下，如果把一只黄油猫从二楼垂直扔下去，那么是黄油猫的小脚先着地，还是黄油猫的背先着地?因此还有人会问，当然是黄油猫的小脚，因为这是黄油猫的天性嘛。不过如果当黄油猫的背上贴了一块黄油面包时，那么这件事情恐怕可就没有那么简单了。因为这个悖论出在，当你把这块黄油吐司没有直接涂上黄油的那一面黏着猫的背部之时。并依照以上的两条主要定律，黄油猫将根本就无法用脚去进行着陆，因为黄油吐司将会永远的在涂上黄油的那一面落地。但是同样的，如果黄油吐司在涂上黄油的那一面根本就无法落地，因为黄油猫将会永远的用脚着陆。结果就如上面这只喵喵了。