数学性质

当n为一个非零的有理数p/q（最简分数形式），则超椭圆为一平面代数曲线。若n为正数，其曲线次数为pq，若n为负数，其曲线次数为2pq。若a和b均为1且n为偶数，则此超椭圆为一n次的费马曲线（英语：Fermat curve），此时超椭圆没有奇点，但一般而言超椭圆中会有有奇点。

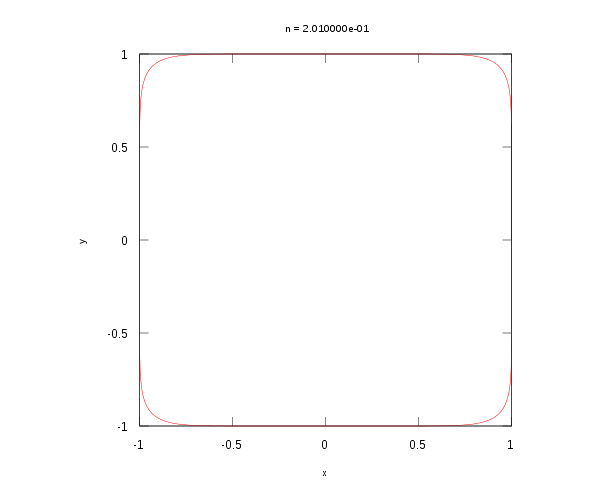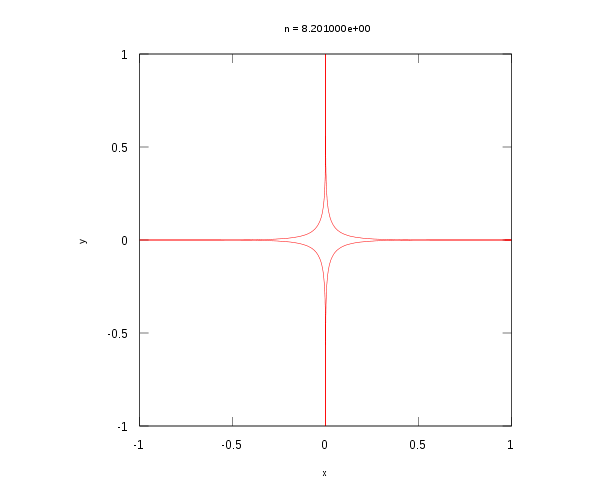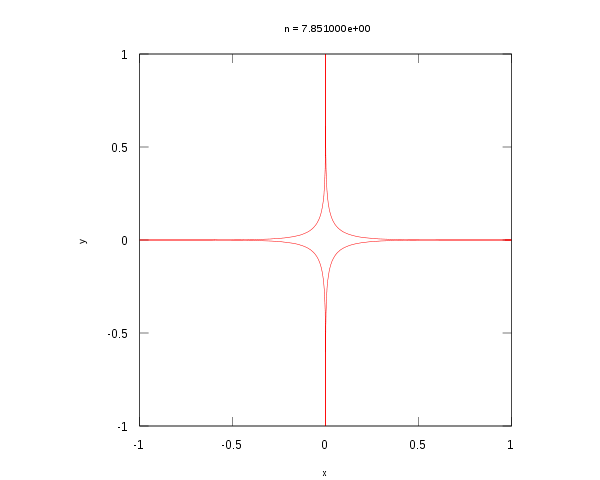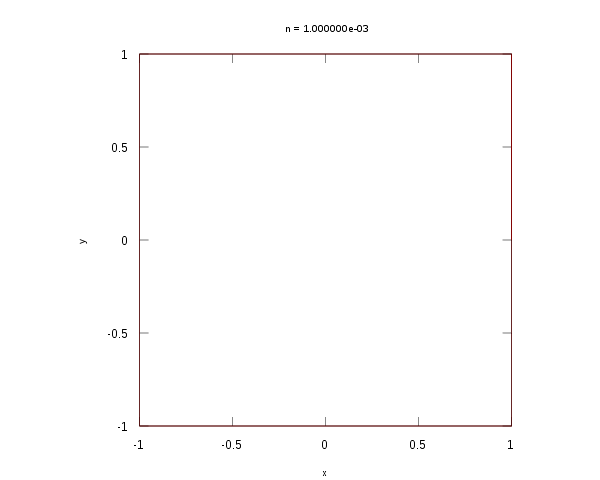
超椭圆的动画

超椭圆的参数方程如下：

或

超椭圆内的面积可以用Γ函数Γ(x)来表示：

其垂足曲线较容易计算，而以下曲线的垂足曲线

可以用极坐标方式来表示：

延伸

广义的超椭圆，m ≠ n.

超椭圆可以延伸为以下的形式：

或

其中的θ θ -->{\displaystyle \theta }不是表示角度，只是方程式的一个参数。

历史

超椭圆在笛卡儿坐标系下的表示式是由1795年出生的法国数学家加布里埃尔·拉梅，由椭圆的方程式扩展而得。

Zapf"s Melior字体的"o"及"O"的轮廓可以用n = log(1/2) / log (7/9) ≈ 2.758的超椭圆来表示

字体设计师赫尔曼·察普夫在1952年设计的Melior字体，利用超椭圆作为字母o的外形。三十年后高德纳设法选择了介于椭圆及超椭圆之间的曲线（两者都用样条函数近似），作为他的Computer Modern字体。

1959年时瑞典斯德哥尔摩提出了其市中心赛格尔广场圆环的设计竞赛。丹麦诗人皮亚特·海恩(1905–1996)的设计以是一个n = 2.5，a/b = 6/5的超椭圆为基础。他的说明如下：

赛格尔广场在1967年完成，而皮亚特·海恩继续在其他的艺术品中使用超椭圆，包括床、碟子、桌子等。皮亚特·海恩将超椭圆以长轴为轴心旋转，形成了一个立体的超级蛋（英语：superegg），其特点是可以平面上直立，不会倒下，因此变成一个特别的玩具。

1968年在巴黎在为越战谈判时，谈判者不满意谈判桌的外形，Balinski、Kieron Underwood及Holt在一封寄给的信件中建议以超椭圆作为谈判桌的外形。1968年由墨西哥城主办奥运时，也以超椭圆为阿兹特克体育场的外形。

托布勒（英语：Waldo R. Tobler）在1973年提出了托布勒超椭圆投影（英语：Tobler hyperelliptical projection），其中的经线就是用超椭圆来表示。

美式足球球队匹兹堡钢人的标志是三个相连的超椭圆。

相关条目

星形线，n = 2/3，且a = b的超椭圆，是四尖瓣的内摆线。

方圆形，n = 4，且a = b的超椭圆，看起来像是“正方形的轮子”。

超公式（英语：Superformula），超椭圆的延伸。

超二次曲面（英语：Superquadrics），三维下的超椭圆。

超椭圆曲线（英语：Superelliptic curve），方程为Y = f(X)的曲线。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。