历史

主要概念来自于陀螺仪，由于第一个 万向接头 由罗伯特·胡克制造，因此又称做 胡克接头 。其实意大利数学家卡尔达诺（Gerolamo Cardano）在此前 一世纪的1545年就已提出了万向接头的想法，但是他是否制造出来实际模型却没有记载。在欧洲，人们也管这一装置叫做卡丹接头（Cardan joint）或者卡丹杆（Cardan shaft）。瑞典人 克里斯托弗·普尔海姆 （ 英语 ： Christopher_Polhem ） 后来重新发明了这种装置，因此在瑞典语中成为它被称为“普尔海姆结”（Polhemsknot）。

运作方式

  万向接头变化图

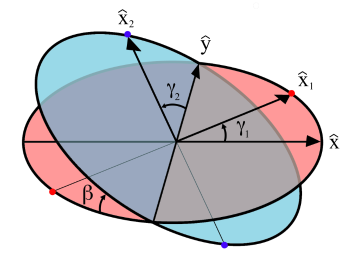
万向接头的主要问题－即使在驱动轴的旋转轴以恒定的速度转动，从动轴在旋转轴变速，造成振动、磨损和速度上的差异，主动轴的速度变化取决于连接的配置，可指定的三个变量：

γ γ --> 1 {\displaystyle \gamma _{1}} ：轴1的旋转角度

γ γ --> 2 {\displaystyle \gamma _{2}} ：轴2的旋转角度

β β --> {\displaystyle \beta } ：两联接轴的偏离角度，若两轴为直线连接，则此角度为0

这些变量在右侧的图中说明。还示出了具有单位矢量的一组固定坐标轴 x ^ ^ --> {\displaystyle {\hat {\mathbf {x} }}} and y ^ ^ --> {\displaystyle {\hat {\mathbf {y} }}} 和每个轴的旋转平面。这些旋转平面垂直于旋转轴线，并且不随轴线旋转而移动。两个轴由未示出的万向节连接。然而，轴1在图中的红色旋转平面上的红点处附接到万向节，并且轴2附接在蓝色平面上的蓝点处。相对于旋转轴固定的坐标系被定义为具有其x轴单位向量 ( x ^ ^ --> 1 {\displaystyle {\hat {\mathbf {x} }}_{1}} and x ^ ^ --> 2 {\displaystyle {\hat {\mathbf {x} }}_{2}} )从原点指向一个连接点。 如图所示， x ^ ^ --> 1 {\displaystyle {\hat {\mathbf {x} }}_{1}} 是成角度的 γ γ --> 1 {\displaystyle \gamma _{1}} 相对于其沿着“x”轴的起始位置和 x ^ ^ --> 2 {\displaystyle {\hat {\mathbf {x} }}_{2}} 是成角度的 γ γ --> 2 {\displaystyle \gamma _{2}} 相对于沿着“y”轴的其起始位置。

x ^ ^ --> 1 {\displaystyle {\hat {\mathbf {x} }}_{1}} 被限制在图中的“红色平面”并与之相关 γ γ --> 1 {\displaystyle \gamma _{1}}

x ^ ^ --> 2 {\displaystyle {\hat {\mathbf {x} }}_{2}} 被限制在图中的“蓝色平面”，并且是在“x”轴上的单位向量的结果 x ^ ^ --> = [ 1 , 0 , 0 ] {\displaystyle {\hat {x}}=[1,0,0]} 通过欧拉角旋转 [ π π --> / 2 , β β --> , 0 {\displaystyle [\pi \!/2\,,\,\beta \,,\,0} ]:

双万向轴

相关

自动倾斜器

传动轴

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。