重力加速度

令 a 1 为事先已知质点的重力加速度。由牛顿第二定律知 F = m 1 a 1 {\displaystyle F=m_{1}\ a_{1}} ， 即 a 1 = F m 1 {\displaystyle a_{1}={\frac {F}{m_{1}}}} 。取代前面方程中的 F

同理亦可得出 a 2 .

依照国际单位制，重力加速度（同其他一般加速度）的单位被规定为米每平方秒(m/s or m s )。非国际单位制的单位有伽利略、[单位g]（见后）以及 英尺每秒的平方。

请注意上述方程中的 a 1 ，质量 m 1 的加速度，在实际上并不取决于 m 1 的取值，即重力加速度大小只与 m 2 和r有关。

具有空间广度的物体

如果被讨论的物体具有空间广度（远大于理论上的质点），它们之间的万有引力可以以物体的各个等效质点所受万有引力之和来计算。在极限上，当组成质点趋近于“无限小”时，将需要求出两物体间的力（矢量式见下文）在空间范围上的积分。

从这里可以得出：如果物体的质量分布呈现均匀球状时，其对外界物体施加的万有引力吸引作用将同所有的质量集中在该物体的几何中心 时的情况相同。（这不适用于非球状对称物体）。

矢量式

地球引力示意图

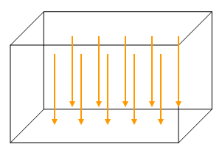
地球附近空间内的引力示意图：在此数量级上地球表面的弯曲可被忽略不计，因此力线可以近似地相互平行并且指向地球的中心

牛顿万有引力定律亦可通过矢量方程的形式进行表述而用以计算万有引力的方向和大小。在下列公式中，以粗体显示的量代表矢量。

可以看出矢量式方程的形式与之前给出的标量式方程相类似，区别仅在于在矢量式中的 F 是一个矢量，以及在矢量式方程的右端被乘上了相应的单位矢量。而且，我们可以看出： F 12 = − F 21 .

同样，重力加速度的矢量式方程与其标量式方程相类似：

引力场

球状星团 M13 证明引力场的存在。

引力场是用于描述在任意空间内某一点的物体每单位质量所受万有引力的矢量场。而在实际上等于该点物体所受的重力加速度。

以下是一个普适化的矢量式，可被应用于多于两个物体的情况（例如在地球与月球之间穿行的火箭）的计算。对于两个物体的情况（比如说物体1是火箭，物体2是地球）来说，我们可以用 r {\displaystyle \mathbf {r} } 替代 r 21 {\displaystyle \mathbf {r} _{21}} 并用 m {\displaystyle m} 替代 m 1 {\displaystyle m_{1}} 来将引力场 g ( r ) {\displaystyle \mathbf {g} (\mathbf {r} )} 表示为：

因此我们可以得到：

该公式不受产生引力场的物体的限制。引力场的单位为力除以质量的单位；在国际单位制上，被规定为N·kg （牛顿每千克）。

牛顿理论存在的问题

尽管牛顿对引力的描述对于众多实践运用来说十分地精确，但它也具有几大理论问题且被证明是不完全正确的。

理论问题

没有任何征兆表明引力的传送媒介可以被识别出，牛顿自己也对这种无法说明的 超距作用 感到不满意（参看后文条目“牛顿定律的局限性”）。

牛顿的理论需要定义引力可以瞬时传播。因此给出了经典自然时空观的假设，这样亦能使约翰内斯·开普勒所观测到的角动量守恒成立。但是，这与爱因斯坦的狭义相对论理论有直接的冲突，因为狭义相对论定义了速度的极限——真空中的光速——在此速度下信号可以被传送。

观测结果的不符

牛顿的理论并不能完全地解释出水星在沿其轨道运动到近日点时出现的进动现象 。牛顿学说的预言（由其它行星的引力拖拽产生）与实际观察到的进动相比每世纪会出现43弧秒的误差。

牛顿的理论预言的引力作用下光线的偏折只有实际观测结果的一半。广义相对论则与观察结果更为接近。

所有物体的引力质量与惯性质量相同的这一观测现象是牛顿的系统所不能解释的。广义相对论则将它作为一个基本条件。更多内容，请参阅条目等效原理。

牛顿定律的局限性

当牛顿非凡的工作使万有引力定律能够为数学公式所表示后，他仍然不满于公式中所隐含的“超距作用”观点。他从来没有在他的文字中“赋予产生这种能力的原因”。在其它情况下，他使用运动的现象来解释物体受到不同力的作用的原因，但是对于引力这种情况，他却无法用实验方法来确认运动产生了引力。此外，他甚至还拒绝对这个由地面产生的力的起因提出假设，而这一切都违背了科学证据的原则。

牛顿对引力的发现埋葬了“哲学家至今仍在愚蠢地试图探索自然”( philosophers have hitherto attempted the search of nature in vain )这句所谓的真理，就同他深信着的“有各种因素”使得“各种迄今未知的原因”是所有“自然现象”的基础。这些基本的现象至今仍在研究中，而且，虽然存在着许多种的假设，最终答案仍然没有找出。 虽然爱因斯坦的假设的确比牛顿的假设更能精确地解释确定案例中万有引力的作用效果，他也从来没有在他的理论中为这种能力赋予一个原因。在爱因斯坦的方程中，“物质告诉空间怎么扭曲，空间告诉物质怎么移动”( matter tells space how to curve, and space tells matter how to move )，但是这个完全异于牛顿世界的新的思想，也不能使爱因斯坦所赋予“产生这种能力的原因”比万有引力定律使牛顿所赋予的原因更能使空间产生扭曲。牛顿自己说：

如果科学最终能够发现引力产生的原因的话，牛顿的希望也将最终被实现。

需要注意的是，这里使用的单词“原因( cause )”并不是“起因( cause )和影响”或者“被告导致( cause )受害者死亡”中所表示的意义。何况，当牛顿使用单词“原因( cause )”时，他（明显地）意指为一种“解释”。或者说，像“牛顿学说的引力是行星运动的原因”这个短语的意思就是牛顿学说的引力解释了行星的运动。参看条目因果。

参见

力

质量

绝对时空观

相对时空观

广义相对论

物理学定律列表

参考文献

注解原理： - Proposition 75, Theorem 35: p.956 - I.Bernard Cohen and Anne Whitman, translators:Isaac Newton, The Principia :Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton"s Principia , by I.Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 ISBN 0-520-08817-4

注解进动： - Max Born (1924), Einstein"s Theory of Relativity (The 1962 Dover edition, page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury, Venus, and Earth.)

注释

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。