波源

一般而言，互不相关的波源无法形成可观察到的干涉图样。例如白炽灯或太阳是由很多互不相关、持续生成的微小发光点所组成，每一个发光点只会作用一段时间Δ Δ -->t≈ ≈ -->10− − -->8− − -->10− − -->9sec{\displaystyle \Delta t\approx 10^{-8}-10^{-9}sec}，发射出一个有限长度的波列，之后，再也不会发光，但在其它位置，又会出现新的发光点。为了要能拍摄到这类光源所产生的由两个波列叠加形成的干涉图样，摄影仪器的时间必须要小于Δ Δ -->t{\displaystyle \Delta t}。在旧时，无法制造出这么高阶的摄影仪器，因此从这类光源很难拍摄到干涉图样。但是，通过适当处理，仍旧可以观察到这些光源的干涉图样。

为了要观察到这些互不相关的波源所形成的干涉图样，必须从这些波源制造出相干性较高的波。有两种方法可以达成这目标：

第一种方法称为“波前分割法”。从微小波源发射出的波，其波前与微小波源之间的距离大致相等。使用具有几条狭缝的档板来过滤从微小波源发射出的波，只要这些狭缝与微小波源之间的距离相等，就可以保证同样的波前入射于这几条狭缝。位于波前的每一点都可以视为一个波源，会发射出次波。因此，从这几条狭缝衍射出来的次波，其相位大致相同。杨氏双缝实验就是借着这方法制成两束相干性较高的光波，这两束光波会在观察屏产生干涉图样。

第二种方法称为“波幅分割法”。用半透射、半反射的半镀银镜，可以将光波一分为二，制造出透射波与反射波，这两束光波非常相似，相干性非常高。假设这两束光波的光程长度不相等，则由于在观察屏的相位不同，会产生明显不同的干涉图样。迈克耳孙干涉仪使用的就是这种方法。

自从激光、激微波的发明以后，物理学者不再为寻找高相干性的光源这问题而烦恼，激光所制造出来的波列通常能维持Δ Δ -->t≈ ≈ -->10− − -->3sec{\displaystyle \Delta t\approx 10^{-3}sec}之久。这给予足够的时间来拍摄干涉图样。

应用

以前，只有在学习光学的杨式双缝实验时，才会接触到相干性这术语。现今许多涉及波动的领域，像声学、电子工程、量子力学等等，都会使用到这术语。许多科技的运作都倚赖相干性质为基础。例如，全息摄影术、音波相位阵列、光学相干断层扫描、天文光学干涉仪、与射电望远镜、等等。

相干性与相关性

两个波的相干性，称为“互相干性”，来自于它们彼此之间的相关程度，也就是说，它们彼此之间的相似程度。互相关函数可以量度互相干性。 互相关函数可以量度从一个波预测另一个波的能力。举例而言，设想完全同步相关的两个波。在任意时间，假若一个波发生任何变化，则另一个波也会做出同样的变化；让这两个波互相干涉，则在任意时间，它们都会展示出完全相长干涉，它们具有完全相干性。互相关函数可以用来支持模式识别系统，例如，指纹识别。

如稍后所述，第二个波不必是另外一个实体，它可能是在不同时间或不同位置的第一个波。这案例所涉及的相关称为“自相干性”；对于这案例，可以用自相关函数来量度自相干性。自相关函数可以用来从带有随机噪声背景的信号中提取出信息信号。

严格定义

假设在点S1、点S2的波扰分别为E~ ~ -->1(t){\displaystyle {\tilde {E}}_{1}(t)}、E~ ~ -->2(t){\displaystyle {\tilde {E}}_{2波浪号)}（波浪号代表复数），则其互相关函数Γ Γ -->~ ~ -->12(τ τ -->){\displaystyle {\tilde {\Gamma }}_{12}(\tau )}为

其中，单书名号表示取时间平均值，T{\displaystyle T}是平均的时间间隔，τ τ -->{\displaystyle \tau }是相对时移。

互相关函数又称为“互相干函数”。理论而言，必需取T{\displaystyle T}趋向于无穷大的极限；然而，实际而言，只要平均的时间间隔比相干时间（大约是有限长度的波列通过某固定点的有限时间）长久很多就行了。

从互相关函数的定义式，可以衍生出自相关函数，又称为“自相干函数”。波E~ ~ -->1(t){\displaystyle {\tilde {E}}_{1}(t)}与相对时移τ τ -->{\displaystyle \tau }的自己波，两者之间的自相干函数为

归一化的互相干函数γ γ -->~ ~ -->12(τ τ -->){\displaystyle {\tilde {\gamma }}_{12}(\tau )}又称为两个波的“复相干度”，以方程表示为

从柯西-施瓦茨不等式可以推导出|γ γ -->~ ~ -->12(τ τ -->)|≤ ≤ -->1{\displaystyle |{\tilde {\gamma }}_{12}(\tau )|\leq 1}。

绝对值|γ γ -->~ ~ -->12(τ τ -->)|{\displaystyle |{\tilde {\gamma }}_{12}(\tau )|}就是“相干度”。当|γ γ -->~ ~ -->12(τ τ -->)|=1{\displaystyle |{\tilde {\gamma }}_{12}(\tau )|=1}时，波E~ ~ -->1{\displaystyle {\tilde {E}}_{1}}与波E~ ~ -->2{\displaystyle {\tilde {E}}_{2}}完全相干；当|γ γ -->~ ~ -->12(τ τ -->)|=0{\displaystyle |{\tilde {\gamma }}_{12}(\tau )|=0}时，两个波完全不相干；当0~ ~ -->12(τ τ -->)|<1{\displaystyle 0 时，两个波部分相干。

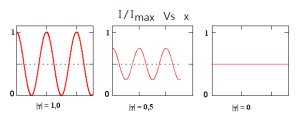
本图展示各种干涉图样的明暗条纹的清晰程度与干涉可见度的关系。纵轴是辐照度除以最大辐照度，横轴是空间坐标。

“干涉可见度”量度干涉图样的明暗条纹的清晰程度，以方程定义，

其中，Imax{\displaystyle I_{max}}、Imax{\displaystyle I_{max}}分别为干涉图样的最大辐照度与最小幅照度。

干涉可见度的范围在0到1之间。假设两个波的振幅相等，则干涉可见度等于相干度：

各种波动实例

下述这些波的共同之处是，它们的物理行为可以用波动方程或推广的波动方程来描述：

绳索的机械波。

液体的表面波。

电缆的电磁波。

声波。

无线电波与微波。

光波。

量子尺寸粒子的物质波。

这些种类的波的物理行为，大多数可以直接测量获得。因此，波与波之间的互相干函数可以很简单地求得。但是，在光学里，不能直接的测量电磁场，因为电磁场的震荡太快，比任何探测器的时间分辨率还要快。可行之道是测量光波的辐照度。

大多数在这条目提到的涉及相干性的概念，都是先在光学领域发展成功，然后再适应于其它领域。因此，许多相干性测量标准都是采用间接地测量，甚至在可以直接测量的领域，都是这样做。

时间相干性

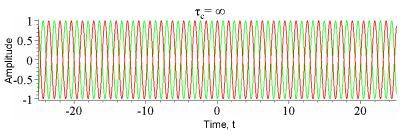
图1：本图显示出，一个单色波的振幅（红色），与延迟了时间τ τ -->{\displaystyle \tau }的自己波的振幅（绿色），这两个振幅随着时间t{\displaystyle t}的演进而变化。这两个波的相干时间是无穷大。因为，对于所有可能延迟时间τ τ -->{\displaystyle \tau }，它们完全相干：|γ γ -->~ ~ -->11(τ τ -->)|=1{\displaystyle |{\tilde {\gamma }}_{11}(\tau )|=1}。

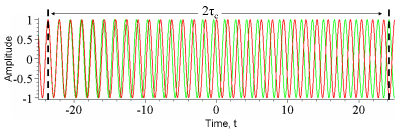
图2：本图显示出，一个相位显著飘移的准单色波的振幅（红色，相干时间为τ τ -->c{\displaystyle \tau _{c}}），与延迟了时间2τ τ -->c{\displaystyle 2\tau _{c}}的自己波的振幅（绿色），这两个振幅随着时间t{\displaystyle t}的演进而变化。在任何给定时间t{\displaystyle t}，红色波会与绿色波互相干涉。但是由于一半时间，红色波与绿色波同相，另一半时间，两个波异相，所以，对于这延迟，经过时间平均后，自相干函数可以近似为0。

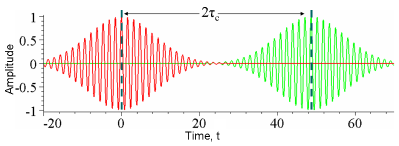
图3：本图显示出，一个波包的振幅（红色）与延迟了时间2τ τ -->c{\displaystyle 2\tau _{c}}的自己波包的振幅（绿色），这两个振幅随着时间t{\displaystyle t}的演进而变化。从本图可以观察到，经过时间τ τ -->c{\displaystyle \tau _{c}}，波包的振幅有显著地改变。在任何瞬时，红色波包与绿色波包是不相关的；当一个波包在做大幅度振荡的时候，另一个波包却是非常的平静。所以，在这里，并没有干涉效应发生。换另一种方法来看，波包并没有重叠于时间，在任何瞬时，最多只有一个波包贡献震荡，不会产生干涉。

一个波E~ ~ -->1(t){\displaystyle {\tilde {E}}_{1}(t)}与延迟了时间τ τ -->{\displaystyle \tau }的自己波，两者之间的自相干函数Γ Γ -->~ ~ -->11(τ τ -->){\displaystyle {\tilde {\Gamma }}_{11}(\tau )}，可以用来量度时间相干性。对应的复相干度为γ γ -->~ ~ -->11(τ τ -->){\displaystyle {\tilde {\gamma }}_{11}(\tau )}，单色为“复时间相干度”。时间相干性可以表达波源的单色性质，可以量度一个波在延迟某时间后干涉自己的能力，因此又称为“纵向相干性”。经过一段延迟时间τ τ -->{\displaystyle \tau }后，假若一个波的相位或波幅开始发生足够显著的变化（因此自相干函数开始显著地减小），则定义此延迟时间为“相干时间”τ τ -->c{\displaystyle \tau _{c}}。有限长度的波列通过某固定点的有限时间大约是相干时间。当τ τ -->=0{\displaystyle \tau =0}时，一个波E~ ~ -->1(t){\displaystyle {\tilde {E}}_{1}(t)}与自己的相干度为|γ γ -->~ ~ -->11(0)|=1{\displaystyle |{\tilde {\gamma }}_{11}(0)|=1}；而当τ τ -->≥ ≥ -->τ τ -->c{\displaystyle \tau \geq \tau _{c}}时，相干度|γ γ -->~ ~ -->11|{\displaystyle |{\tilde {\gamma }}_{11}|}会显著地减小，显示在观察屏的干涉图样也会变得模糊不清。“相干长度”Lc{\displaystyle L_{c}}定义为，在相干时间τ τ -->c{\displaystyle \tau _{c}}内，波所能传播的距离，又称为“纵向相干长度”。

相干时间与带宽的关系

由于周期的倒数是频率，一个波在越短时间内，变的不自相干（τ τ -->c{\displaystyle \tau _{c}}越小），则波的带宽Δ Δ -->f{\displaystyle \Delta f}越大。两个物理量的关系方程为

用波长λ λ -->=c/f{\displaystyle \lambda =c/f}来表达，

用数学表述，这结果可以从傅里叶变换推导出来。自相干函数的傅里叶变换就是功率谱（英语：power spectrum）（每个频率的辐照度）。

实例

试想下述四个关于时间相干性的实例：

对于任何时间间隔，一个单色波都是完全的自相干（参阅图1）。

反过来说，一个相位迅速飘移的波，其相干时间必定很短（参阅图2）。

类似地，具有较宽频域的脉冲波（英语：pulse wave）（一种波包），由于振幅迅速地变化，所以，相干时间很短（参阅图3）。

白光拥有非常宽的频域，是一种振幅与相位都迅速变化的波。由于相干时间很短（10周期左右），常被称为“不相干波”。

白光的带宽大约为3×10Hz，因此相干时间为3×10s，相干长度非常短，大约只有900nm。普通放电灯的带宽也很宽阔，因此相干长度也相当短，大约为几个mm数量级。国际标准Kr低气压放电灯的相干长度比较长，大约为0.3m。

激光通常是最单色的光源。高度的单色性意味着相干长度很长。例如，单模氦氖激光（英语：helium-neon laser）能够发射相干长度接近400m的光。特别稳定性氦氖激光的相干长度可以达到1.5×10m。

全息摄影需要用到长相干时间的光。由于具有脉冲高能量与较长的相干时间这两种优点，红宝石激光时常被应用于全息摄影。相对比较，光学相干断层扫描使用短相干时间的光。

测量方法

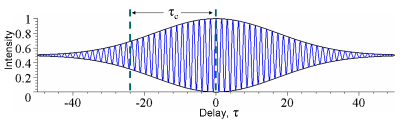
图4：输入波为图 (2)或图 (3)的波，在辐照度干涉仪输出点侦测到的，经过时间平均后的辐照度，以延迟时间τ τ -->{\displaystyle \tau }的函数形式绘制。假设将延迟时间改变半个周期，则干涉会从建设性转换为摧毁性，或从摧毁性转换为建设性。黑色曲线显示出干涉包络线，这是相干度的曲线。虽然，图 (2)或图 (3)的波有不同的持续期，它们有同样的相干时间。

在光学里，时间相干性可以用干涉仪来测量，例如，迈克耳孙干涉仪或马赫-曾德尔干涉仪。干涉仪先将输入波复制，延后τ τ -->{\displaystyle \tau }时间，然后将输入波与复制波合并为输出波，再用辐照度探测器来测量经过时间平均后的输出波辐照度，得到的数据，稍加运算，可以求得干涉可见度。这样，可以知道延迟时间为τ τ -->{\displaystyle \tau }的相干度。对于大多数的天然光源，由于相干时间超短于探测器的时间分辨率，探测器自己就可以完成时间平均工作。

思考图 (3)案例，在相干时间τ τ -->c{\displaystyle \tau _{c}}内，波的辐照度显著地涨落不定。假设延迟时间为2τ τ -->c{\displaystyle 2\tau _{c}}，则一个无穷快的探测器所测量出的辐照度也会显著地涨落不定。对于这案例，可以手工计算辐照度的时间平均值来求得时间相干性。

空间相干性

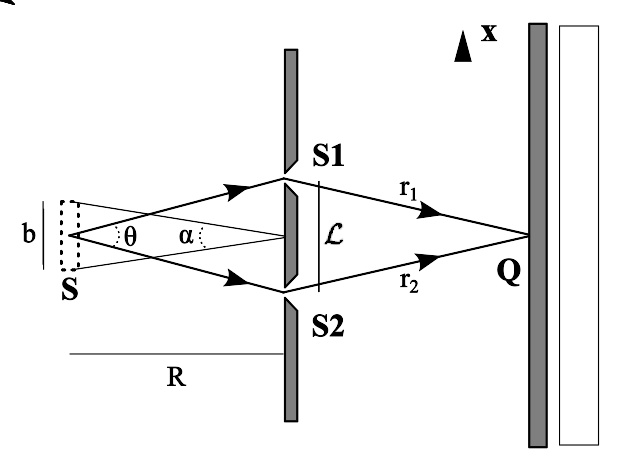
波源绵延有限尺寸的杨氏双缝实验示意图。最右边的干涉图样是由单独点波源产生的图样。

为了展示出显著的干涉图样，杨氏双缝实验所使用的光源必须具有空间相干性。光学影像系统与天文望远镜的制作必需考虑到光源的空间相干性。

空间相干性与波源的有限尺寸有关。这可以用杨式双缝实验来解释。在典型的杨式双缝实验里，只存在有一个点光源S，其所发射出的单色光，在通过不透明挡板的位于点S1、点S2的两条狭缝之后，会在观察屏显示出干涉图样。现在将这实验加以延伸，将点光源S改为绵延有限尺寸b{\displaystyle b}的线光源。从做实验获得的结果，物理学者发觉，假定线光源与挡板之间的距离R{\displaystyle R}足够远，则若要在观察屏的中央轴区域显示出干涉图样，必须先满足以下条件：

其中，θ θ -->{\displaystyle \theta }是点S1、点S2对于顶点S的夹角。λ λ -->{\displaystyle \lambda }是光波的平均波长。

注意到θ θ -->≈ ≈ -->L/R{\displaystyle \theta \approx {\mathcal {L}}/R}、α α -->≈ ≈ -->b/R{\displaystyle \alpha \approx b/R}；其中，L{\displaystyle {\mathcal {L}}}是两个狭缝之间的距离，α α -->{\displaystyle \alpha }是有限尺寸光源对于档板中央轴交点的夹角。所以，必须满足条件

因此，可以估算这问题的“横向相干长度”为Lc=λ λ -->/α α -->{\displaystyle {\mathcal {L}}_{c}=\lambda /\alpha }。假若两个狭缝之间的距离大于Lc{\displaystyle {\mathcal {L}}_{c}}，则干涉图样会消灭殆尽。对于三维案例，可以使用物理量“相干面积”，以方程表示为Ac=λ λ -->2/α α -->2{\displaystyle {\mathcal {A}}_{c}=\lambda ^{2}/\alpha ^{2}}。

在许多物理系统里，像水波或光波一类的波可以传播于一维或多维的空间。空间相干性量度位于点S1、点S2的的两个波扰，经过时间平均后，彼此相互干涉的能力。更精确地说，空间相干性是这两个波扰除去了延迟时间因素之后的互相关函数。假设某波前的波幅为常数，则在其任意两个位置的波扰，彼此之间都具有完全空间相干性。

继续思考杨氏双缝实验，只专注于档板与观察屏之间的状况。假设点S1、点S2的两个波扰分别为E~ ~ -->1(t){\displaystyle {\tilde {E}}_{1}(t)}、E~ ~ -->2(t){\displaystyle {\tilde {E}}_{2}(t)}，则其互相干函数Γ Γ -->~ ~ -->12(τ τ -->)=⟨ ⟨ -->E~ ~ -->1(t+τ τ -->)E~ ~ -->2∗ ∗ -->(t)⟩ ⟩ -->{\displaystyle {\tilde {\Gamma }}_{12}(\tau )=\langle {\tilde {E}}_{1}(t+\tau ){\tilde {E}}_{2}^{\,*}(t)\rangle }与点S1、点S2的位置和延迟时间τ τ -->{\displaystyle \tau }有关。由于在观察屏的干涉图样，其中心点Q是中央轴与观察屏的交点，从点S1、点S2同时发射的光波，会在同时抵达点Q，延迟时间为

其中，r1{\displaystyle r_{1}}、r2{\displaystyle r_{2}}分别是从S1、点S2到点Q的距离，c{\displaystyle c}是光速。

因此，除去了延迟时间因素，互相干函数Γ Γ -->~ ~ -->12(0){\displaystyle {\tilde {\Gamma }}_{12}(0)}可以量度在点S1、点S2的两个波扰的空间相干性。复相干度γ γ -->~ ~ -->12(0){\displaystyle {\tilde {\gamma }}_{12}(0)}称为在点S1、点S2的两个波扰的“复空间相干度”。

实例

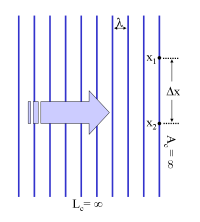
图5：一个单色平面波，相干长度与相干面积为无穷值。

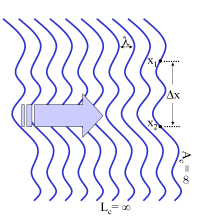
图6：一个波前不规则的单色波。因为在点X1与点X1后面λ整数倍数之处的波幅永远相同，相干长度为无穷值，因为在点X1与点X2的波幅永远相同，相干面积也为无穷值。

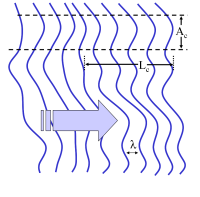
图7：一个波前不规则的波，相干长度与相干面积为有限值。

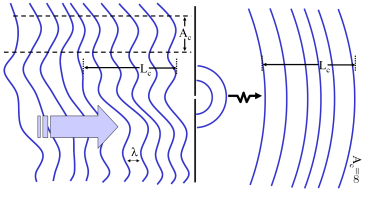
图8：一个波前不规则、相干长度与相干面积为有限值的波，入射于具有一条狭缝的档板。入射波穿过狭缝后，衍射出来的波，其空间相干性会增加。经过传播一段距离，在离狭缝较远处，圆形波前的波近似于平面波。相干面积变为无穷值，而相干长度不变。

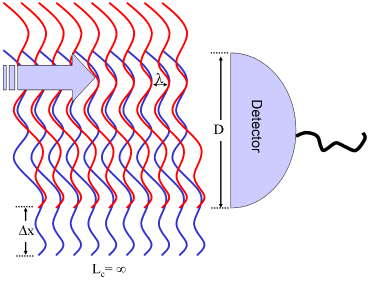
图9：两个同样的波，在空间里传播。一个波是另外一个波的位移，两个波的相干长度与相干面积分别为无穷值。两个波的结合，在某些位置，会相长干涉，在另外一些位置，会摧毁性干涉。经过空间平均，探测器所观察到的干涉图样，其干涉可见度会减低。例如，一个未校准的马赫-曾德尔干涉仪就会出现这种状况。

试想一个电灯泡的钨丝，从其不同位置会独立地发射出毫无固定相位关系的光波。仔细观察，在任意时间，光波的剖面都毫无规律可言。每经过一段相干时间τ τ -->c{\displaystyle \tau _{c}}，光波的剖面都会概率性地变化。电灯泡是一个白光光源，相干时间τ τ -->c{\displaystyle \tau _{c}}很短，是一个空间不相干光源。

位于美国新墨西哥州的综合孔径射电望远镜甚大天线阵。

电波望远镜天线阵的空间相干性很高，在天线阵对端的每两根天线所发射出的光波，彼此之间都有特别设计的固定相位关系。

激光产生的光波的时间相干性与空间相干性通常都很高，其相干度依激光的性质而定。

全息摄影术的运作，需要时间相干与空间相干的光波。它的发明者，伽博·丹尼斯，在激光还没有被发明前，就已经成功地做出全息图。他将水银灯的发射线激发出的单色光，通过针孔过滤器，制成全息摄影术所需要的相干光波。

2011年2月，物理学者发现，冷却至接近绝对零度的氦原子，当变为玻色-爱因斯坦凝聚时，它们的物理行为会如同激光发射出的相干光束一样。

波谱相干性

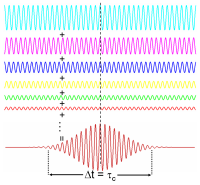
几个不同频率的波（在光学里，不同颜色的光波），假若是相干的，则会因相互干涉而形成一个脉冲波。

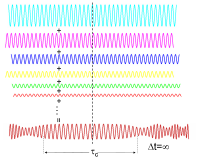
几个波谱不相干的波因相互干涉而形成的波，其相位与波幅都会随机变化。

不同频率的波（在光学里，不同颜色的光波），假若有固定的相对相位关系，则会因干涉而形成一个脉冲波（参阅傅里叶变换）。反过来说，假若不同频率的波是不相干的，则结合在一起它们会形成像白光或白噪声一类的波。脉冲波的时间持续期Δ Δ -->t{\displaystyle \Delta t}被带宽Δ Δ -->f{\displaystyle \Delta f}限制，依据关系方程：

这关系方程也可以从傅里叶变换推导出。对于量子尺寸的粒子，这是海森堡不确定原理的必然结果。

测量光的波谱相干性，需要用到非线形光波干涉仪（英语：nonlinear optical interferometer），像辐照度相关器（英语：Intensity optical correlator）、频域分辨光学开关或波谱相位干涉仪（英语：Spectral phase interferometry for direct electric-field reconstruction）。

量子相干性

在量子力学里，物质具有波动性（参阅德布罗意假说）。例如，杨氏双缝实验也可以用电子来完成。从电子源发射出的每一个电子可以穿过两条狭缝中的任何一条狭缝，因此，有两种抵达观察屏最终位置的方法可供选择。一种方法是将狭缝S1关闭，电子只能穿过狭缝S2；另一种方法是将狭缝S2关闭，电子只能穿过狭缝S1。每一种方法可以设定为一个特别的量子态。由于这两个量子态会相互干涉，因而影响电子抵达侦测屏最终位置的概率分布，也因此形成了观察屏的干涉图样。这相互干涉的能力展现出粒子的“量子相干性”。

假若，试图探测电子到底是经过哪一条狭缝。那么，两个量子态的相位关系会不再存在。这双态系统就会被退相干化。这现象显示出量子系统的互补性。

大尺寸（宏观）量子相干会导致新颖奇异的现象，称为宏观量子现象（英语：macroscopic quantum phenomena）。例如，激光、超导现象、超流体等等，都是高度相干的量子系统，它们产生的效应可以在宏观尺寸观察到。超流体现象是玻色-爱因斯坦凝聚。所有组成凝聚的粒子都同相，可以用单独一个量子波函数来描述。

换另一方面，薛定谔猫思想实验强调，不能任意地将量子相干用在宏观案例。但是，物理学者于2009年成功地在机械共振器（英语：resonator）的运动里观测到量子相干现象。

参阅

相干态

量子退相干

原子相干性（英语：atomic coherence）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。