原理

作图公法

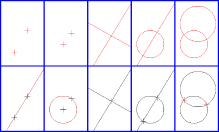
作图公法

以下是尺规作图中可用的基本方法，也称为作图公法，任何尺规作图的步骤均可分解为以下五种方法：

通过两个已知点可作一直线。

已知圆心和半径可作一个圆。

若两已知直线相交，可求其交点。

若已知直线和一已知圆相交，可求其交点。

若两已知圆相交，可求其交点。

问题

古希腊三大难题

古希腊三大难题是早期希腊数学家特别感兴趣的三个问题。由于我们的现代几何学知识是从希腊发源的，因此这三个古典几何问题在几何学中有着很高的地位。它们分别是：

在欧几里得几何学的限制下，以上三个问题都不可能解决。 据说，这些问题据欧几里得几何作图求解的不可能性的最早严格证明是旺采尔(P. L. Wantzel)于1837年给出的。

正多边形作法

只使用直尺和圆规，作正五边形。

只使用直尺和圆规，作正六边形。

只使用直尺和圆规，作正七边形——这个看上去非常简单的题目，曾经使许多著名数学家都束手无策，因为正七边形已被证明是不能由尺规作出的。

只使用直尺和圆规，作正九边形，此图也不能作出来，因为单用直尺和圆规，是不足以把一个角分成三等份的。

1832年，Richelot与Schwendewein给出正257边形的尺规作法。

1900年左右，Hermes花费十年的功夫用尺规作图作出正65537边形，他的手稿装满一大皮箱，可以说是最复杂的尺规作图。

四等分圆周

这道题只准许使用圆规，要求参与者将一个已知圆心的圆周4等分。这道题传言是拿破仑·波拿巴拟出，向全法国数学家挑战的。这道题已被证明有解。

延伸

圆规作图

1672年，乔治·莫尔（Georg Mohr）证明：如果把“作直线”解释为“作出直线上的2点”，那么凡是尺规能作的，单用圆规也能作出，拿破仑问题就是一个例子。

直尺作图

只用直尺所能作的图其实不多，但在已知一个圆和其圆心的情况下，那么凡是尺规能作的，单用直尺也能作出。

生锈圆规（即半径固定的圆规）作图

生锈圆规作图，已知两点 A {\displaystyle A} 、 B {\displaystyle B} ，找出一点 C {\displaystyle C} 使得 A B = B C = C A {\displaystyle AB=BC=CA} 。

已知两点 A {\displaystyle A} 、 B {\displaystyle B} ，只用半径固定的圆规，求作 C {\displaystyle C} 使 C {\displaystyle C} 是线段 A B {\displaystyle AB} 的中点。

尺规作图，是古希腊人按“尽可能简单”这个思想出发的，能更简洁的表达吗？顺着这思路就有了更简洁的表达。

从给定的两点出发时，生锈圆规作图完全等价于尺规作图。

但是，“从给定的两点出发”这一条件必不可少，在有多个已知点的条件下，锈规作图的能力还有待研究。

二刻尺作图

将条件放宽，允许使用有刻度的直尺，可以三等分角或做出正七边形等一般尺规做图所做不到的事。

允许使用长度等于1的线段

已知两条线段AB、AC，可以作出一条线段的长度等于两条线段长度之乘积AB×AC。

尺规作图的程式

C.a.R.-Java程式

GRACE-在线Java程式

Geometric Drawing Pad-在线Java程式

Ruler & compass-在线程式

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。