概述

高斯定律表明，电场的散度等于总电荷密度 ρ ρ --> t o t a l {\displaystyle \rho _{total}} 除以电常数：

电极化强度的散度等于负束缚电荷密度 − − --> ρ ρ --> b o u n d {\displaystyle -\rho _{bound}} ：

而总电荷密度等于束缚电荷密度加上自由电荷密度 ρ ρ --> f r e e {\displaystyle \rho _{free}} ：

所以，电势移的散度等于自由电荷密度 ρ ρ --> f r e e {\displaystyle \rho _{free}} ：

这与高斯定律的方程类似。假设，只给定自由电荷密度 ρ ρ --> f r e e {\displaystyle \rho _{free}} ，或许可以用高斯方法来计算电势移 D {\displaystyle \mathbf {D} } 。但是，在这里，不能使用这方法。只知道自由电荷密度 ρ ρ --> f r e e {\displaystyle \rho _{free}} ，有时候仍旧无法计算出电势移。思考以下关系式：

假设电场为不含时电场， ∇ ∇ --> × × --> E = 0 {\displaystyle \nabla \times \mathbf {E} =0} ，则

假若 ∇ ∇ --> × × --> P ≠ ≠ --> 0 {\displaystyle \nabla \times \mathbf {P} \neq 0} ，则虽然设定 ρ ρ --> f r e e = 0 {\displaystyle \rho _{free}=0} ，电势移仍旧不等于零： D ≠ ≠ --> 0 {\displaystyle \mathbf {D} \neq 0} ！

举例而言，拥有固定电极化强度 P {\displaystyle \mathbf {P} } 的永电体，其内部不含有任何自由电荷，但是内在的电极化强度 P {\displaystyle \mathbf {P} } 会产生电场。

只有当问题本身具有某种对称性，像球对称性或圆柱对称性等等，才能够直接使用高斯方法，从自由电荷密度计算出电势移与电场。否则，必需将电极化强度 P {\displaystyle \mathbf {P} } 和边界条件纳入考量。

线性电介质

“线性电介质”，对于外电场的施加，会产生线性响应。例如，铁电材料是非线性电介质。假设线性电介质具有各向同性，则其电场与电极化强度的关系式为

其中， χ χ --> e {\displaystyle \chi _{e}}电极化率极化率。

将这关系式代入电势移的定义式，可以得到

其中， ϵ ϵ --> {\displaystyle \epsilon } 是电容率。

所以，电势移与电场成正比；其比率是电容率。另外，

假设这电介质具有均匀性，则电容率 ϵ ϵ --> {\displaystyle \epsilon } 是常数：

定义相对电容率 ϵ ϵ --> r {\displaystyle \epsilon _{r}} 为

相对电容率与电极化率有以下的关系：

各向异性线性电介质的电容率是个张量。例如，晶体的电容率通常必需用张量来表示。

应用范例

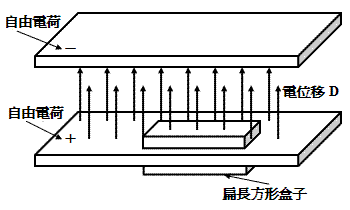
平行板电容器的两片平板导体分别含有的正负自由电荷，会产生电势移。借着一个扁长方形盒子，可以用高斯定律来解释电势移与自由电荷的关系。

如右图所示，平行板电容器是由互相平行、以空间或电介质相隔的两片平板导体构成的电容器。假设上下两片平板导体分别含有负电荷与正电荷，含有的电荷量分别为 − − --> Q {\displaystyle -Q} 、 + Q {\displaystyle +Q} 。又假设两片平板导体之间的间隔距离超小于平板的长度与宽度，则可以视这两片平板导体为无限平面；做简单计算时，不必顾虑边缘效应。由于系统的对称性，可以应用高斯定律来计算电势移，其方向必定是从带正电平板导体指向带负电平板导体，而且垂直于平板导体；又由于平板导体含有的电荷是自由电荷，不需要知道电介质的性质，就可以应用关于自由电荷的高斯定律来计算电势移。

先计算带正电平板导体所产生的电势移。试想一个扁长方形盒子，其顶面和底面分别在这平板导体的两边，平行于平板导体；而盒子的其它四个侧面都垂直于平板导体。根据关于自由电荷的高斯定律，

其中， S {\displaystyle \mathbb {S} } 是扁长方形盒子的闭合表面， D + {\displaystyle \mathbf {D} _{+}} 是带正电平板导体所产生的电势移， d a {\displaystyle d\mathbf {a} } 是微小面元素。

由于扁长方形盒子的四个侧面的面矢量都与 D + {\displaystyle \mathbf {D} _{+}} 矢量相垂直，它们对于积分的贡献是零；只有盒子的顶面和底面对于积分有贡献：

其中， A {\displaystyle A} 是盒子顶面、底面的面积。

所以， D + {\displaystyle \mathbf {D} _{+}} 矢量的方向是从带正电平板导体垂直地向外指出，大小为

类似地，可以计算出带负电平板导体所产生的电势移； D − − --> {\displaystyle \mathbf {D} _{-}} 矢量的方向是垂直地指向带负电平板导体，大小为

应用叠加原理，可以计算这两片带电平板导体一起产生的电势移。在这两片平板导体之间， D + {\displaystyle \mathbf {D} _{+}} 和 D − − --> {\displaystyle \mathbf {D} _{-}} 的方向相同；应用叠加原理，电势移的大小等于平板导体的表面电荷密度： D = Q / A {\displaystyle D=Q/A} 。在两片平板导体的共同上方或共同下方， D + {\displaystyle \mathbf {D} _{+}} 和 D − − --> {\displaystyle \mathbf {D} _{-}} 的方向相反；应用叠加原理，电势移的大小等于零。

假设电介质的电容率为 ϵ ϵ --> {\displaystyle \epsilon } ，则在两片平板导体电场，电场的大小为

假设两片平板导体的间隔距离为 d {\displaystyle d} ，则电压 V {\displaystyle V} 为

这平行板电容器的电容 C {\displaystyle C} 为

参阅

《论法拉第力线》

《论物理力线》

位移电流

电磁波方程

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。