历史

Tijms (2004, p.169) 写到：

棣莫佛－拉普拉斯定理

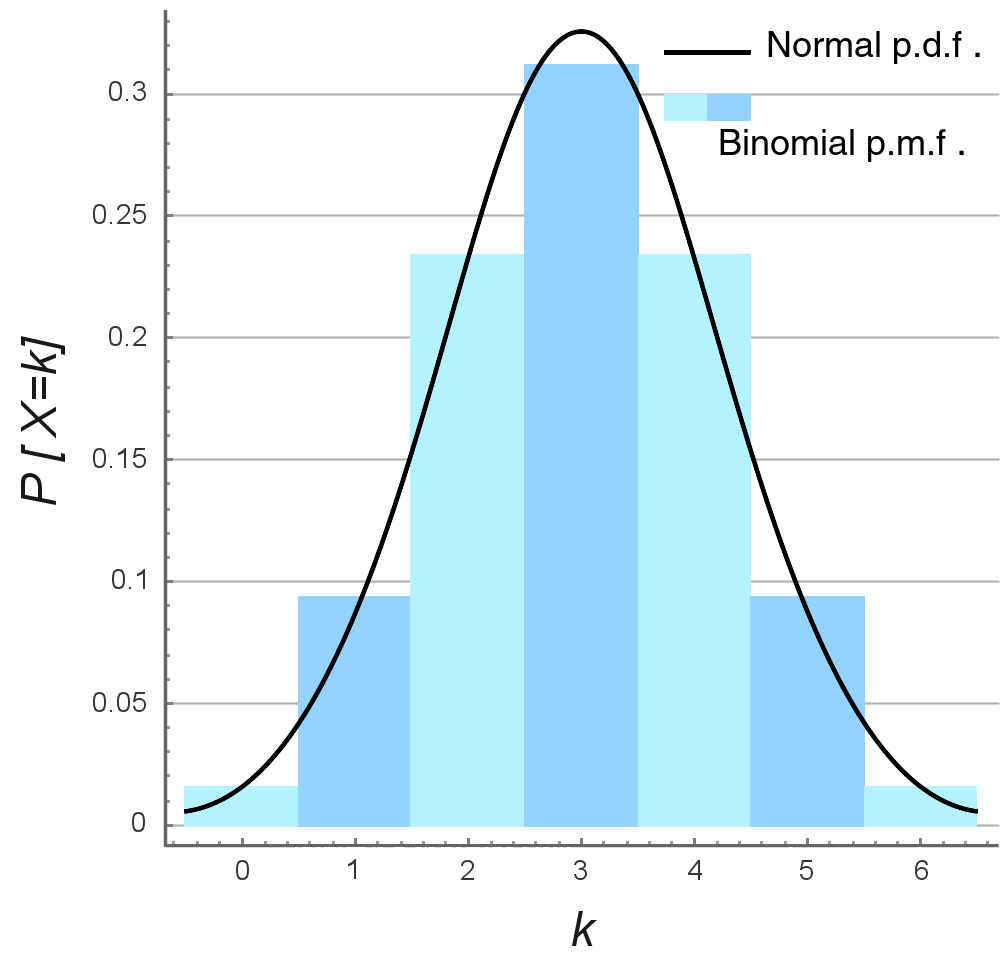
用正态分布逼近二项分布

棣莫佛－拉普拉斯（de Moivre - Laplace）定理是中央极限定理的最初版本，讨论了服从二项分布的随机变量序列。它指出，参数为n, p的二项分布以np为均值、np(1-p)为方差的正态分布为极限。

内容

若μ μ -->n{\displaystyle \mu _{n}}是n次伯努利实验中事件A出现的次数，0<p<1{\displaystyle 0

，则对任意有限区间

：

(i)当a≤ ≤ -->xk≡ ≡ -->k− − -->npnpq≤ ≤ -->b{\displaystyle a\leq {x_{k}}\equiv {\frac {k-np}{\sqrt {npq}}}\leq {b}}（xkk{\displaystyle {x_{k}}{k}}及n→ → -->∞ ∞ -->{\displaystyle n\to {\infty }}时，一致地有

P{μ μ -->n=k}÷ ÷ -->(1npq⋅ ⋅ -->12π π -->e− − -->12xk2)→ → -->1{\displaystyle P\{\mu _{n}=k\}\div ({\frac {1}{\sqrt {npq}}}\cdot {\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x_{k}^{2}})\to 1}

(ii)当n→ → -->∞ ∞ -->{\displaystyle n\to \infty }时，一致地有

P{a≤ ≤ -->μ μ -->n− − -->npnpq∫ ∫ -->abφ φ -->(x)dx{\displaystyle P\{a\leq {\frac {\mu _{n}-np}{\sqrt {npq}}}， 其中φ φ -->(x)=12π π -->e− − -->x22(− − -->∞ ∞ --><x).{\displaystyle \varphi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {x^{2}}{2}}}(-\infty

在高尔顿板问题上的应用

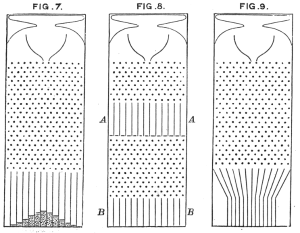
高尔顿绘制的高尔顿板模型，其中的小球显出钟形曲线。

棣莫弗－拉普拉斯定理指出二项分布的极限为正态分布。高尔顿板可以看作是伯努利试验的实验模型。如果我们把小球碰到钉子看作一次实验，而把从右边落下算是成功，从左边落下看作失败，就有了一次p=12{\displaystyle p={\frac {1}{2}}}的伯努利试验。小球从顶端到底层共需要经过n排钉子，这就相当于一个n次伯努利试验。小球的高度曲线也就可以看作二项分布随机变量的概率密度函数。因此，中央极限定理解释了高密顿板小球累积高度曲线为什么是正态分布独有的钟形曲线。

林德伯格－列维定理

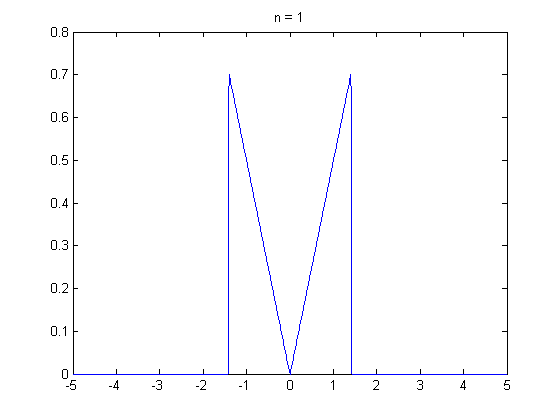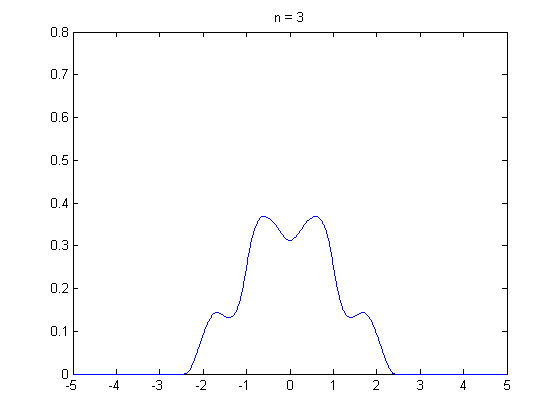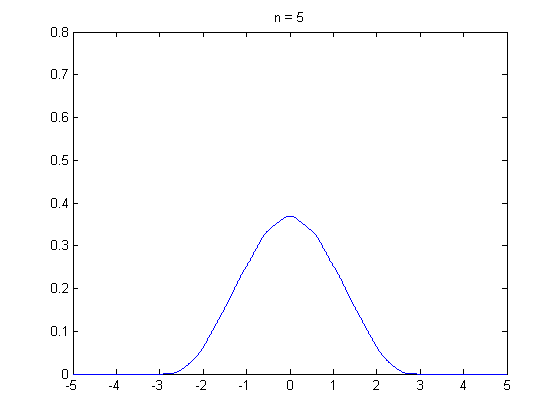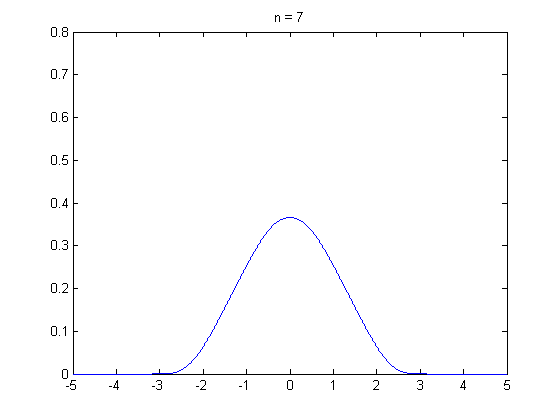
中央极限定理的动态展示，独立同分布随机变量之和趋近正态分布。

林德伯格－列维（Lindeberg-Levy）定理，是棣莫佛－拉普拉斯定理的扩展，讨论独立同分布随机变量序列的中央极限定理。它表明，独立同分布、且数学期望和方差有限的随机变量序列的标准化和以标准正态分布为极限：

内容

设随机变量X1,X2,⋯ ⋯ -->,Xn{\displaystyle X_{1},X_{2},\cdots ,X_{n}}独立同分布， 且具有有限的数学期望和方差E(Xi)=μ μ -->{\displaystyle E(X_{i})=\mu }，D(Xi)=σ σ -->2≠ ≠ -->0(i=1,2,⋯ ⋯ -->,n){\displaystyle D(X_{i})=\sigma ^{2}\neq 0(i=1,2,\cdots ,n)}。记

X¯ ¯ -->=1n∑ ∑ -->i=1nXi{\displaystyle {\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}}，ζ ζ -->n=X¯ ¯ -->− − -->μ μ -->σ σ -->/n{\displaystyle \zeta _{n}={\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}}，则 limn→ → -->∞ ∞ -->P(ζ ζ -->n≤ ≤ -->z)=Φ Φ -->(z){\displaystyle \lim _{n\rightarrow \infty }P\left(\zeta _{n}\leq z\right)=\Phi \left(z\right)}

其中Φ Φ -->(z){\displaystyle \Phi (z)}是标准正态分布的分布函数。

证明

记Xk− − -->μ μ -->{\displaystyle X_{k}-\mu }的特征函数为φ φ -->(t){\displaystyle \varphi (t)}，根据傅里叶变换，样本空间中的褶积在特征函数空间变为乘积，因此ζ ζ -->n{\displaystyle \zeta _{n}}的特征函数为[φ φ -->(tσ σ -->n)]n{\displaystyle {\left[\varphi {\left({\frac {t}{\sigma {\sqrt {n}}}}\right)}\right]}^{n}}.由于E(Xk)=μ μ -->,D(Xk)=σ σ -->2{\displaystyle E(X_{k})=\mu ,D(X_{k})=\sigma ^{2}}故φ φ -->′(0)=0,φ φ -->″(0)=− − -->σ σ -->2.{\displaystyle \varphi "(0)=0,\varphi ""(0)=-\sigma ^{2}.}因此

φ φ -->(t)=1− − -->12σ σ -->2t2+o(t2){\displaystyle \varphi (t)=1-{\frac {1}{2}}\sigma ^{2}t^{2}+o(t^{2})}

所以

[φ φ -->(tσ σ -->n)]n=[1− − -->12nt2+o(t2n)]n→ → -->e− − -->t2/2{\displaystyle {\left[\varphi {\left({\frac {t}{\sigma {\sqrt {n}}}}\right)}\right]}^{n}=\left[1-{\frac {1}{2n}}t^{2}+o\left({\frac {t^{2}}{n}}\right)\right]^{n}\to {e^{-t^{2}/2}}}

由于e− − -->t2/2{\displaystyle e^{-t^{2}/2连续函数续函数，它对应的分布函数为Φ Φ -->(Z){\displaystyle \Phi (Z)}，因此由逆极限定理知

limn→ → -->∞ ∞ -->P(ζ ζ -->n≤ ≤ -->z)→ → -->Φ Φ -->(z){\displaystyle \lim _{n\rightarrow \infty }P\left(\zeta _{n}\leq z\right)\to \Phi \left(z\right)}

定理证毕。

林德伯格-费勒定理

林德伯格－费勒定理，是中央极限定理的高级形式，是对林德伯格－列维定理的扩展，讨论独立，但不同分布的情况下的随机变量和。它表明，满足一定条件时，独立，但不同分布的随机变量序列的标准化和依然以标准正态分布为极限：

内容

记随机变量序列Xi{\displaystyle X_{i}}（Xi{\displaystyle X_{i}}独立但不一定同分布，E[Xi]=0{\displaystyle E[X_{i}]=0}且有有限方差）部分和为

Sn=∑ ∑ -->i=1nXi{\displaystyle S_{n}=\sum _{i=1}^{n}X_{i}}

记

si2=Var(Xi){\displaystyle s_{i}^{2}={\rm {Var}}(X_{i})}

σ σ -->n2=∑ ∑ -->i=1nsi2=Var(Sn){\displaystyle \sigma _{n}^{2}=\sum _{i=1}^{n}s_{i}^{2}={\rm {Var}}(S_{n})}.

如果对每个ϵ ϵ -->>0{\displaystyle \epsilon >0}，序列满足

limn→ → -->∞ ∞ -->1σ σ -->n2∑ ∑ -->i=1nE[Xi2;{|Xi|>ϵ ϵ -->σ σ -->n}]=0{\displaystyle \lim _{n\rightarrow \infty }{1 \over \sigma _{n}^{2}}\sum _{i=1}^{n}E[X_{i}^{2};\{|X_{i}|>\epsilon \sigma _{n}\}]=0}

则称它满足林德伯格（Lindeberg）条件。

满足此条件的序列趋向于正态分布，即

Sn/σ σ -->n→ → -->dN(0,1){\displaystyle S_{n}/\sigma _{n}{\stackrel {d}{\rightarrow }}N(0,1)}

同时，该条件也是期望为零、方差有限的独立变量之和趋于正态分布的必要条件。

与之相关的是李雅普诺夫（Lyapunov）条件：

E[|Xi|3],limn→ → -->∞ ∞ -->1σ σ -->n3∑ ∑ -->i=1nE[|Xi|3]=0{\displaystyle E[|X_{i}|^{3}]

满足李雅普诺夫条件的序列，必满足林德伯格条件。

证明

在此只对较强的李雅普诺夫条件给出证明。

以下证明对每一实数t{\displaystyle t}，特征函数满足φ φ -->Sn/σ σ -->n(t)→ → -->e− − -->t2/2{\displaystyle \varphi _{S_{n}/\sigma _{n}}(t)\rightarrow e^{-t^{2}/2}}。

|φ φ -->Sn/σ σ -->n(t)− − -->e− − -->t2/2|=|∏ ∏ -->k=1nφ φ -->Xk(t/σ σ -->n)− − -->∏ ∏ -->k=1ne− − -->t2sk2/2σ σ -->n2|≤ ≤ -->∑ ∑ -->k=1n|φ φ -->Xk(t/σ σ -->n)− − -->e− − -->t2sk2/2σ σ -->n2|{\displaystyle \left|\varphi _{S_{n}/\sigma _{n}}(t)-e^{-t^{2}/2}\right|=\left|\prod _{k=1}^{n}\varphi _{X_{k}}(t/\sigma _{n})-\prod _{k=1}^{n}e^{-t^{2}s_{k}^{2}/2\sigma _{n}^{2}}\right|\leq \sum _{k=1}^{n}\left|\varphi _{X_{k}}(t/\sigma _{n})-e^{-t^{2}s_{k}^{2}/2\sigma _{n}^{2}}\right|}

泰勒展开，上式可近似为

∑ ∑ -->k=1n|i3t3E[Xk3]6σ σ -->n3+t4sk48σ σ -->n4|≤ ≤ -->|t|36σ σ -->n3∑ ∑ -->k=1nE[|Xk|3]+t48σ σ -->n4∑ ∑ -->k=1nsk4≤ ≤ -->|t|36σ σ -->n3∑ ∑ -->k=1nE[|Xk|3]+t48max1≤ ≤ -->k≤ ≤ -->nsk2σ σ -->n2{\displaystyle \sum _{k=1}^{n}\left|{\frac {i^{3}t^{3}E[X_{k}^{3}]}{6\sigma _{n}^{3}}}+{\frac {t^{4}s_{k}^{4}}{8\sigma _{n}^{4}}}\right|\leq {|t|^{3} \over 6\sigma _{n}^{3}}\sum _{k=1}^{n}E[|X_{k}|^{3}]+{\frac {t^{4}}{8\sigma _{n}^{4}}}\sum _{k=1}^{n}s_{k}^{4}\leq {|t|^{3} \over 6\sigma _{n}^{3}}\sum _{k=1}^{n}E[|X_{k}|^{3}]+{\frac {t^{4}}{8}}\max _{1\leq k\leq n}{s_{k}^{2} \over \sigma _{n}^{2}}}

由李雅普诺夫条件，当n→ → -->∞ ∞ -->{\displaystyle n\rightarrow \infty }时，第一项收敛于零。

令kn=argmax1≤ ≤ -->k≤ ≤ -->nsk2/σ σ -->n2{\displaystyle k_{n}={\rm {arg}}\max _{1\leq k\leq n}s_{k}^{2}/\sigma _{n}^{2}}，则由李雅普诺夫不等式，

(skn/σ σ -->n)3/2≤ ≤ -->E[|Xkn/σ σ -->n|3]≤ ≤ -->1σ σ -->n3∑ ∑ -->k=1nE[|Xk|3]{\displaystyle (s_{k_{n}}/\sigma _{n})^{3/2}\leq E[|X_{k_{n}}/\sigma _{n}|^{3}]\leq {\frac {1}{\sigma _{n}^{3}}}\sum _{k=1}^{n}E[|X_{k}|^{3}]}

因此第二项也收敛于零。

证毕。

参阅

大数定律

重对数律

参考文献

李贤平，概率论基础（第二版），高等教育出版社

Olav Kallenberg，现代概率论基础（第二版），Springer（2002）。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。