一维谐振子

哈密顿算符与能量本征态

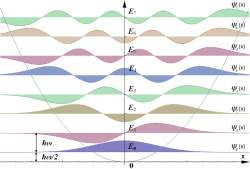
  能量最低的六个束缚本征态的波函数表征（n = 0到7）。横轴表示位置x。此图未经归一化。

在一维谐振子问题中，一个质量为m的粒子，受到一位势 V ( x ) = 1 2 m ω ω --> 2 x 2 {\displaystyle V(x)={\frac {1}{2}}m\omega ^{2}x^{2}} 。此粒子的哈密顿算符为

其中x为位置算符，而p为动量算符 ( p = − − --> i ℏ ℏ --> d d x ) {\displaystyle \left(p=-i\hbar {d \over dx}\right)} 。第一项代表粒子动能，而第二项代表粒子处在其中的势能。为了要找到能阶以相对应的能量本征态，必须解所谓的“定态薛定谔方程”：

在坐标基底下可以解这个微分方程，用到幂级数方法。可以见到有一族的解：

最先六个解（n = 0到5）展示在右图。函数 H n {\displaystyle H_{n}} 为埃尔米特多项式：

注意到不应将之与哈密顿算符搞混，尽管哈密顿算符也标作H。相应的能阶为

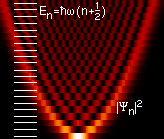
  束缚本征态之概率密度|ψn(x)|²，从最底部的基态（n = 0）开始，往上能量逐渐增加。横轴表示位置x，而较亮的色彩代表较高的概率密度。

值得注意的是能谱，理由有三。首先，能量被“量子化”（quantized），而只能有离散的值——即 ℏ ℏ --> ω ω --> {\displaystyle \hbar \omega } 乘以1/2, 3/2, 5/2……等等。这是许多量子力学系统的特征。在尔后的“阶梯算符”段落，将对此现象做更详细的检视。再者，可有的最低能量（当n = 0）不为零，而是 ℏ ℏ --> ω ω --> / 2 {\displaystyle \hbar \omega /2} ，被称为“基态能量”或零点能量。在基态中，根据量子力学，一振子执行所谓的“零振动”（ oscillations）且其平均动能是正值。这样的现象意义重大但并不那么显而易见，因为通常能量的零点并非一个有意义的物理量，因为可以任意选择；有意义的是能量差。虽然如此，基态能量有许多的意涵，特别是在量子引力。最后一个理由式能阶值是等距的，不像玻尔模型或盒中粒子问题那样。

注意到基态的概率密度集中在原点。这表示粒子多数时间处在势阱的底部，合乎对于一几乎不带能量之状态的预期。当能量增加时，概率密度变成集中在“经典转向点”（classical turning points），其中状态能量等同于势能。这样的结果与经典谐振子相一致；经典的描述下，粒子多数时间处在（而更有机会被发现在）转向点，因为在此处粒子速度最慢。因此满足对应原理。

阶梯算符方法

前述的幂级数解虽然直观，但显得相当繁复。阶梯算符方法起自保罗·狄拉克，允许抽像求得能量本征值，而不用直接解微分方程。此外，此法很容易推广到更复杂的问题，尤其是在量子场论中。跟从此方法，定义算符a与其伴随算符（adjoint）a：

算符a并非厄米算符（Hermitian），以其与伴随算符a并不相同。

算符a与a有如下性质：

在推导a形式的过程中，已用到算符x与p（代表可观测量）为厄米算符这样的事实。这些可观测量算符可以被表示为阶梯算符的线性组合：

x与p算符遵守下面的等式，称之为正则对易关系：

方程中的方括号是常用的标记机器，称为交换子、交换算符或对易算符，其定义为

利用上面关系，可以证明如下等式：

现在，让 | ψ ψ --> E 〉 {\displaystyle \left|\psi _{E}\right\rangle } 代表带有能量E的能量本征态。任何右括矢量（ket）与自身的内积必须是非负值，因此

将aa以哈密顿算符表示：

因此 E ≥ ≥ --> ℏ ℏ --> ω ω --> / 2 {\displaystyle E\geq \hbar \omega /2} 。注意到当（ a | ψ ψ --> E 〉 {\displaystyle a\left|\psi _{E}\right\rangle } ）为零右括矢量（亦即：长度为零的右括矢量），则不等式饱和而 E = ℏ ℏ --> ω ω --> / 2 {\displaystyle E=\hbar \omega /2} 。很直观地，可以检查到存在有一状态满足此条件——前面段落所提到的基态（n = 0）。

利用上面等式，可以指出a及a与H的对易关系：

因此要是（ a | ψ ψ --> E 〉 {\displaystyle a\left|\psi _{E}\right\rangle } ）并非零右括矢量，

类似地，也可以指出

换句话说，a作用在能量为E的本征态，而产生出——还多了一个常数乘积——另一个能量为 E − − --> ℏ ℏ --> ω ω --> {\displaystyle E-\hbar \omega } 的本征态，而a作用在能量为E的本征态，产生出另一个能量为 E + ℏ ℏ --> ω ω --> {\displaystyle E+\hbar \omega } 的本征态。因为这样，a称作降算符而a称作升算符。两者合称阶梯算符。在量子场论中，a与a也分别称作消灭算符与创生算符，以其分别摧毁与创造粒子——对应于能量量子。

给定任何能量本征态，可以拿降算符a作用在其上，产生了另一个能量少了 ℏ ℏ --> ω ω --> {\displaystyle \hbar \omega } 的本征态。重复使用降算符，似乎可以产生能量本征态其能量低到E = −∞。不过这样就就与早先的要求 E ≥ ≥ --> ℏ ℏ --> ω ω --> / 2 {\displaystyle E\geq \hbar \omega /2} 相违背。因此，必须有一最底的能量本征态——基态，标示作 | 0 〉 {\displaystyle \left|0\right\rangle } （勿与零右括矢量混淆），使得

在这情况下，继续使用降算符只会产生零右括矢量，而不是产生额外的能量本征态。此外，还指出了

最后，透过将升算符作用在 | 0 〉 {\displaystyle \left|0\right\rangle } 上，并且乘上适当的归一化因子，可以产生出一个能量本征态的无限集合 { | 0 〉 , | 1 〉 , | 2 〉 , . . . , | n 〉 , . . . } {\displaystyle \left\{\left|0\right\rangle ,\left|1\right\rangle ,\left|2\right\rangle ,...,\left|n\right\rangle ,...\right\}} 使得

这方法也能够用来很快地找到量子谐振子的基态波函数。只要将消灭算符作用于基态， a | 0 〉 = 0 {\displaystyle a\left|0\right\rangle =0} 变为

所以，

这个方程的解为，经过归一化，

自然长度与能量尺度

量子谐振子拥有自然长度与自然能量两个自然尺度，可以用来简化问题。这可以透过无量纲化来得到。结果是如果以 ℏ ℏ --> ω ω --> {\displaystyle \hbar \omega } 为单位来测量能量，以及 ( ℏ ℏ --> / ( m ω ω --> ) ) 1 / 2 {\displaystyle \left(\hbar /\left(m\omega \right)\right)^{距离2}} 为单位来测量距离，则薛定谔方程变成：

且能量本征态与本征值变成

为了避免混淆，在此文中不采用这些自然单位。不过，这用法在执行运算上总会因便利性而迟早被使用。

案例：双原子分子

在双原子分子中，自然频率可以发现为[1]：

其中

N {\displaystyle N} 维谐振子

一维谐振子很容易地推广到 N {\displaystyle N} 维。在一维中，粒子的位置是由单一坐标x来指定的。在 N {\displaystyle N} 维中，这由 N {\displaystyle N} 个位置坐标所取代，以 x 1 , x 2 , … … --> , x N {\displaystyle x_{1},\,x_{2},\,\dots ,\,x_{N}} 标示。对应每个位置坐标有个动量，标示为p1, ..., pN。这些算符之间的正则对易关系为

系统的哈密顿算符为

从这个哈密顿量的形式，可以发觉， N {\displaystyle N} 维谐振子明确地可比拟为 N {\displaystyle N} 个质量相同，弹性常数相同，独立的一维谐振子。在这案例里，变数 x 1 , x 2 , … … --> , x N {\displaystyle x_{1},\,x_{2},\,\dots ,\,x_{N}} 是 N {\displaystyle N} 个粒子的位置坐标。这是反平方连心位势的一个优良的特性，允许位势被分离为 N {\displaystyle N} 个项目，每一个项目只跟一个位置坐标有关。

这观察使得问题的解答变的相当简单。对于一个集合的量子数 { n } {\displaystyle \{n\}} ，一个 N {\displaystyle N} 维谐振子的能量本征函数 〈 〈 --> x | ψ ψ --> { n } 〉 〉 --> {\displaystyle \langle \mathbf {x} |\psi _{\{n\}}\rangle } 等于 N {\displaystyle N} 个一维本征函数 〈 〈 --> x i | ψ ψ --> n i 〉 〉 --> {\displaystyle \langle x_{i}|\psi _{n_{i}}\rangle } 的乘积：

采用阶梯算符方法，定义 N {\displaystyle N} 组阶梯算符，

类似前面所述的一维谐振子案例，可以证明每一个 a i {\displaystyle a_{i}} 与 a i † † --> {\displaystyle a_{i}^{\dagger }} 算符将能量分别降低或升高 ℏ ℏ --> ω ω --> {\displaystyle \hbar \omega } 。哈密顿量是

这量子系统的能阶 E {\displaystyle E} 是

其中，正整数 n i {\displaystyle n_{i}} 是 | ψ ψ --> n i 〉 〉 --> {\displaystyle |\psi _{n_{i}}\rangle } 的量子数。

如同一维案例，能量是量子化的。 N {\displaystyle N} 维基态能阶是一维基态能阶的 N {\displaystyle N} 倍。只有一点不同，在一维案例里，每一个能阶对应于一个单独的量子态。在 N {\displaystyle N} 维案例里，除了底态能阶以外，每一个能阶都是简并的，都对应于多个量子态。

简并度可以很容易地计算出来。例如，思考三维案例，设定 n = n 1 + n 2 + n 3 {\displaystyle n=n_{1}+n_{2}+n_{3}} 。每一个 n {\displaystyle n} 相同的量子态，都会拥有相同的能量。给予 n {\displaystyle n} ，首先选择一个 n 1 {\displaystyle n_{1}} 。那么， n 2 + n 3 = n − − --> n 1 {\displaystyle n_{2}+n_{3}=n-n_{1}} ，有 n − − --> n 1 + 1 {\displaystyle n-n_{1}+1} 个值，从 0 {\displaystyle 0} 到 n − − --> n 1 {\displaystyle n-n_{1}} ，可以选择为 n 2 {\displaystyle n_{2}} 的值。 n 3 {\displaystyle n_{3}} 的值自动的设定为 n − − --> n 1 − − --> n 2 {\displaystyle n-n_{1}-n_{2}} 。因此，简并度是

对于 N {\displaystyle N} 维案例，

案例：三维均向谐振子

球对称的三维均向谐振子可以用分离变数法来求解。这方法类似于氢原子问题里的方法，只有球对称位势不一样：

其中， μ μ --> {\displaystyle \mu } 是这问题的质量。由于 m {\displaystyle m} 会被用磁量子数量子数，所以，用 μ μ --> {\displaystyle \mu } 来标记质量。

这问题的薛定谔方程为

薛定谔方程的全部解答写为

其中，

能量本征值是

能量通常可以用一个量子数 n {\displaystyle n} 来描述：

由于 k {\displaystyle k} 是个正整数，假若 n {\displaystyle n} 是偶数，那么，角量子数也是偶数：

假若 n {\displaystyle n} 是奇数，那么，角量子数也是奇数：

磁量子数 m {\displaystyle m} 满足不等式

对于每一个 n {\displaystyle n} 与 l {\displaystyle l} ，存在 2 l + 1 {\displaystyle 2l+1} 个不同的量子态。每一个量子态都有不同的磁量子数 m {\displaystyle m} 。因此， n {\displaystyle n} 的兼并度是

其中，总和的指数 l {\displaystyle l} 的初始值是 i = n   m o d   2 {\displaystyle i=n\ mod\ 2} 。

这结果与先前的方程相同。

耦合谐振子

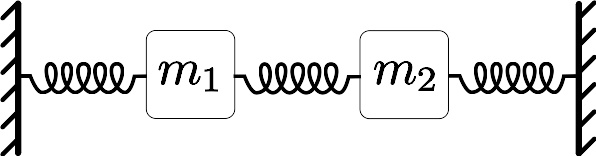
  两个质点的耦合谐振子

设想 N {\displaystyle N} 个相同质量的质点，以弹簧连结为一条一维的线形链条。标记每一个质点的离开其平衡点的位置为 x 1 , x 2 , … … --> , x N {\displaystyle x_{1},\,x_{2},\,\dots ,\,x_{N}} （也就是说，假若一个质点 k {\displaystyle k} 位于其平衡点，则 x k = 0 {\displaystyle x_{k}=0} ）。整个系统的哈密顿量是

其中， x 0 = 0 {\displaystyle x_{0}=0} 。

很奇妙地，这个问题可以用坐标变换来变换成一组独立的谐振子，每一个独立的谐振子对应于一个独特的晶格集体波震动。这些波震动表现出类似粒子般的性质，称为声子。许多固体的离子晶格都会产生声子。在固体物理学里，这方面的理论对于许多现象的研究与了解是非常重要的。

参阅

自由粒子

无限深方形阱

有限深方形阱

有限位势垒

球对称位势

Delta位势垒

参考文献

Griffiths, David J. Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. 2004. ISBN 0-13-111892-7. 

垒球iboff, Richard L. Introductory Quantum Mechanics. Addison-Wesley. 2002. ISBN 978-0-8053-8714-8. 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。