-
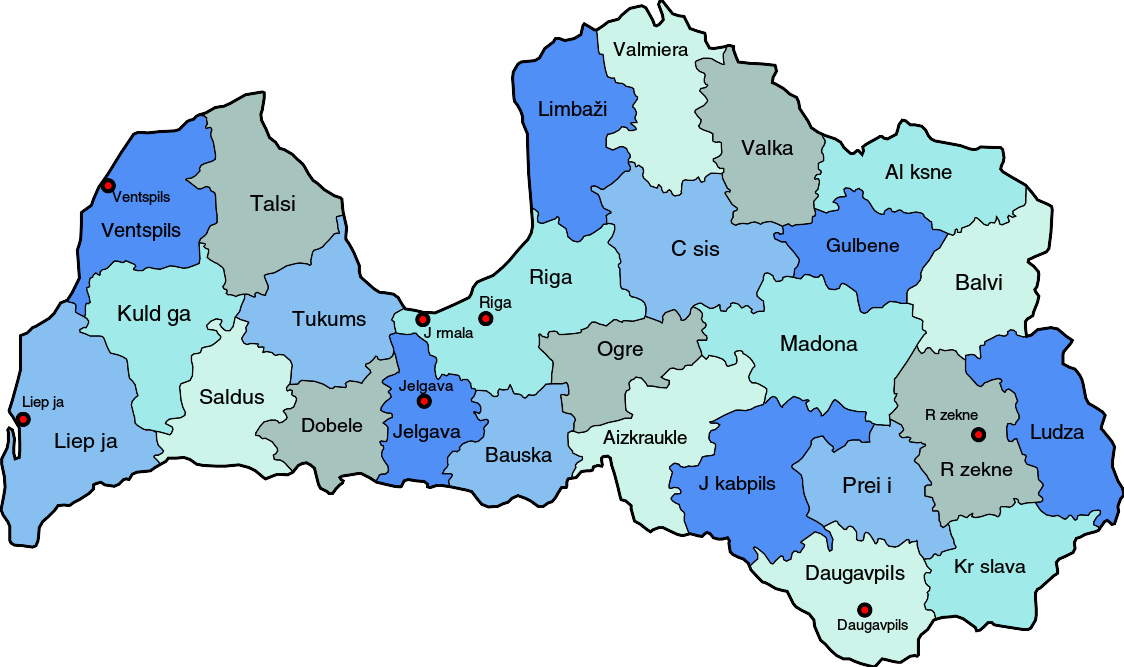
拉脱维亚行政区划
直辖市里加Rīga(首都)陶格夫匹尔斯Daugavpils叶卡布皮尔斯Jēkabpils叶尔加瓦Jelgava尤尔马拉Jūrmala利耶帕亚Liepāja雷泽克内Rēzekne瓦尔米耶拉Valmiera文茨皮尔斯Ventspils自治市旧版行政区划2009年7月1日前,拉脱维亚分为26个县(rajons),以及7个直辖市。2009年前的拉脱维亚行政区划艾兹克劳克莱县(Aizkraukle)阿卢克斯内县(Alūksne)巴尔维县(Balvi)包斯卡县(Bauska)采西斯县(Cēsis)陶格夫匹尔斯市(Daugavpils)陶格夫匹尔斯县(Daugavpils)多贝莱县(Dobele)古尔贝内县(Gulbene)叶卡布皮尔斯县(Jēkabpils)叶尔加瓦市(Jelgava)叶尔加瓦县(Jelgava)尤尔马拉市(Jūrmala)克拉斯拉瓦县(Krāslava)库尔迪加县(Kuldīga)利...
人物百科 | 2017-10-16 -
梅塔特隆
塔木德中的梅塔特隆与《塔木德》相关的以利沙·本·阿布亚(英语:ElishabenAbuyah)(ElishabenAbuyah,被认为是犹太教异端的犹太教士)说过,他进入天堂时,看见梅塔特隆和一班拉比在静坐,于是他看着自己认为是真正的神的梅塔特隆说:“天上真的有两个大国在!”(ThereareindeedtwopowersinHeaven!),拉比们解释说,梅塔特隆不得不让自己坐,因为他的职能是天堂的抄写员,写下以色列的事迹。以诺书中的梅塔特隆在《以诺三书》中有一段描述:梅塔特隆在以诺和雅列面前显现,并说:“祂称我为“仅次于上主的存在”,是整个天国里最高等的存在,因为祂写了“我的名字就是祂的名字”的字句。”——《以诺三书》12:5这本书的作者拉比·以实玛利(英语:RabbiIshmael)也曾描述梅塔特隆如何引导以诺上天堂。另外,以诺三书也写了梅塔特隆以两种方式使以诺成为天使,分别是让他成...
人物百科 | 2017-10-16 -
嘉绒语
语法嘉绒语的动词形态相当丰富,除了时态,还表示人称范畴:动词的人称和数与主语/宾语一致。在汉藏语系里,除了嘉绒语,有许多语言也呈现动词的人称标记,例如景颇语。有的学者甚至怀疑,原始汉藏语可能有相同的动词人称标记,但是这个标记系统在汉语、藏语和缅甸语里消失了,只保留在比较原始的语言里。在汉藏语系里,藏语和汉语具有悠久的文献传统,却丢失了原始语一些很重要的特征,反而处于边缘地区的语言比较接近原始语。以下是四土话(马尔康县的方言)的人称标记,以动词ka-no“赶”为例(这个动词和汉语“让”是同源词-“让”日母漾韵,上古汉语*naŋ-s,四土话-o有时候来自*-aŋ,这两个词溯源于原始汉藏语*naŋ)。横格表示宾语,竖格表示主语,例如:ta-no-ntʃ=“我、我们俩、我们要把你们俩撵出去”同源词参见茶堡话尔龚语拉坞戎语藏语康方言东部土语参考资料黄良荣、孙红开2002.《汉嘉戎语词典北京》:民族出...
人物百科 | 2017-10-16 -
爱丁堡公爵
爱丁堡公爵列表斯图亚特王朝(1566–1702)奥尔登堡王朝(1702–1714)汉诺威王朝(1714–1837)韦廷王朝(1840–1861)萨克森-科堡-哥达王朝(1901–1917)温莎王朝(1917–1952)格吕克斯堡王朝(1952–现今)爱丁堡公爵,第一次册立(1566年)苏格兰王储詹姆斯(1566年生)爱丁堡公爵,第二次册立(1702年)丹麦的乔治亲王(1653年生)爱丁堡公爵,第三次册立(1714年)汉诺威选帝侯乔治(1660年生)爱丁堡公爵,第四次册立(1840年)萨克森-科堡-哥达家族的艾伯特亲王(1819年生)爱丁堡公爵,第五次册立(1901年)王储爱德华亲王(1841年生)爱丁堡公爵,第六次册立(1952年)第一代爱丁堡公爵菲利普亲王(1921年生)继承顺序罗彻斯公爵查理斯(1948年生),菲利普亲王长子剑桥公爵威廉王子(1982年生),查理斯王子长子剑桥乔治王子(...
人物百科 | 2017-10-16 -
玛窦·霍普金斯
人物事迹他出生于萨福克郡的大威翰,曾经当过送货人。有人认为他是清教牧师詹姆斯霍普金斯的一个儿子,亦有人认为他曾经是一名律师,但几乎没有证据可以证明以上这些假说。根据他的论文“女巫搜查法”记载,他的女巫猎手的生涯是在1664年五月他在科尔切斯特附近一个名叫曼宁翠的地方听见妇女们谈论她们遇见恶魔的经历以后开始的。在霍普金斯的指控下,19名女巫嫌疑人被绞死,另外四名则死于监狱中。此后霍普金斯奔走于英格兰东部,他声称,出于某种原因,最高法院已正式委托他进行搜查并捕猎女巫的活动。在1645至1647年间,他的猎巫事业进一步扩大。因为酷刑,即使仅仅是尝试,在英格兰也是非法的,于是,他使用其他多种方法处理犯人,目的是从犯人口中得到对巫术罪行的告白。他通过剥夺她们的睡眠,这种不流血的方法折磨她们。“因为拒绝洗礼的女巫,会因为超自然的力量而从水中浮起”,借着这个理论,他将犯人沉入水中观察她们是浮起或是下沉。...
人物百科 | 2017-10-16 -
位置向量
位置矢量(位矢)从坐标原点指向质点所在位置的矢量称为位置矢量。假设坐标系是直角坐标系,坐标轴为x-轴、y-轴与z-轴,则质点的位置向量标记为(x,y,z){displaystyle(x,,y,,
人物百科 | 2017-10-16 -
五逆罪
部派佛教五逆杀母杀父:父母生身,弑父母大违孝顺双亲老师尊长大人、诸佛的教导。杀阿罗汉出佛身血:如提婆达多欲以大石杀害释迦牟尼佛,以代之领导僧团的历史事件。包括毁佛像因为前世时释迦牟尼和提婆达多互为兄弟佛为了争遗产把提婆推下悬崖再以大石击碎所以今世有如此果报出佛身血就是驱使故意使佛的身体流血破和合僧:破坏修六和敬(见僧伽)的修行众(不分出家在家,皆为“僧团”)的和谐无诤。意思就是破坏出家人的和谐大乘佛教五逆犯小乘五逆罪之一。盗毁常住:自为或教唆他人破坏盗取塔寺、经像等三宝之物。诽谤大乘:诽谤声闻、缘觉以及大乘法(谤法)。杀害出家人或妨碍出家人修行:如歌利王凌迟忍辱仙人的本生谭。不信因果:主张所有心行皆无业报,或不畏果报,自行或教唆他人行十恶之事。五逆罪与往生《无量寿经》阿弥陀佛四十八愿之本愿——第十八愿“十念必生”末后有一句“唯除五逆,诽谤正法”,乍看犯五逆罪者不得往生西方极乐世界;但在《观...
人物百科 | 2017-10-16 -
莫比乌斯变换
简介莫比乌斯变换是定义在扩充复平面上的(扩充复平面是指在普通的复平面加入无穷远点构成的集合)扩充复平面可以看做是一个球面,它的另一个名称就是黎曼球面。每个莫比乌斯变换都是从黎曼球面到它自身的一一对应的共形变换。事实上,所有这样的变换都是莫比乌斯变换。所有莫比乌斯变换的集合在函数复合作用下构成一个群,称为“莫比乌斯群”,记作M(C^^-->){\displaystyle{\mathcal{M}}({\widehat{\mathbb{C}}})}。这个群是黎曼球面(作为一个黎曼曲面)的自同构群,因此有时也被记作:莫比乌斯群同构于三维双曲空间中的保向等距同构群,因此在三维双曲空间中的子流形的研究中占有重要地位。定义莫比乌斯变换的常见形式为:其中a、b、c、d是任何满足ad−bc≠0的复数(当ad=bc的时候这个表达式退化成一个常数,通常约定常数函数不是莫比乌斯变换)。当c≠0时,定义这样便将莫比...
人物百科 | 2017-10-16 -
费边战术
典故古罗马的费边将军(亦作法比乌斯),在前217年特拉西梅诺湖战役中罗马军队被汉尼拔带领的迦太基军队惨败之后他被选为独裁官。因为此时的迦太基军队已经远离本土,所以不能持久作战,费边指出尽管罗马缺乏足够的资源胜利,但是汉尼拔军队的策略目的只有罗马陷落才可能成功。尽管迦太基军队从北非获取几乎是无尽的补给,但补给线太长。所以罗马军采用迂回战术,并不与敌人正面决战,而是利用熟悉地形的优势在山区与敌人周旋,消耗迦太基军。使迦太基军队如果决意进攻罗马,就必须放弃地中海港口。同时罗马还不断小规模骚扰南欧,干扰敌人补给线,效果良好。这种战术以后就被称为“费边战术”,对历史影响巨大。但费边的战术引起了罗马人的不满,他们想借兵力优势迅速打败迦太基人。于是元老院派执政官鲍路斯和瓦罗接替费边,在坎尼进行决战,就是著名的坎尼战役,结果惨败于迦太基军。案例游击战参看费边主义费边社
人物百科 | 2017-10-16 -

十二平均律
历史西蒙·斯特芬作于1605年左右的手稿VandeSpieghelingdersingconst公元400年左右,中国南朝数学家何承天提出世界历史上最早有记载的十二平均律数列900849802758715677638601570536509.5479450(原文:……黄钟长九寸,太簇长八寸二厘,林钟长六寸一厘,应钟长四寸七分九厘强)。意大利的物理学家伽利略·伽利莱的父亲伽利略·文森佐曾试图解决十二平均率问题,但他用的倍率是18:17而不是212{\displaystyle{\sqrt[{12}]{2}}},因此自乘12次后只得1.98556,不是2,八度走了音,他的系统只可算近似十二音阶平均律。1605年荷兰数学家西蒙·斯特芬在一篇未完成的手稿“VandeSpieghelingdersingconst”提出用1/212{\displaystyle{\sqrt[{12}]{1/2}}}计算十...
人物百科 | 2017-10-16




