该协议的历史

迪菲－赫尔曼密钥交换是在美国密码学家惠特菲尔德·迪菲和马丁·赫尔曼的合作下发明的，发表于1976年。它是第一个实用的在非保护信道中创建共享密钥（英语：Shared secret）方法。它受到了瑞夫·墨克的关于公钥分配工作的影响。约翰·吉尔（英语：John Gill (climber)）（John Gill）提出了离散对数问题的应用。该方案首先被英国GCHQ的马尔科姆·J·威廉森（英语：Malcolm J. Williamson）（Malcolm J. Williamson）在稍早的几年前发明，但是GCHQ直到1997年才决定将其公开，这时在学术界已经没有了研究这个算法的热潮了。

这个方法被发明后不久出现了RSA，另一个进行公钥交换的算法。它使用了非对称加密算法。

2002年，马丁·赫尔曼写到：

描述了这个算法的美国专利 4,200,770，已经于1997年4月29日后过期，专利文件表明了Hellman、Diffie和Merkle是算法的发明者。

描述

迪菲－赫尔曼通过公共信道交换一个信息，就可以创建一个可以用于在公共信道上安全通信的共享秘密（shared secret）。

以下解释它的过程（包括算法的数学部分）：

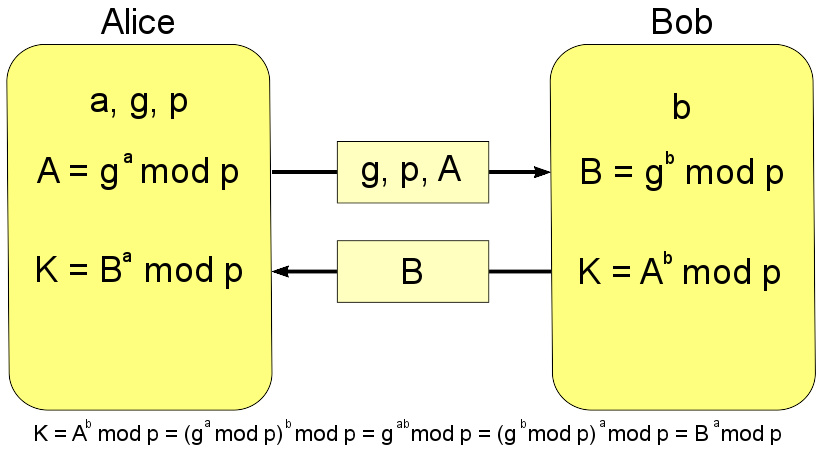
Diffie–Hellman 密钥交换

最简单，最早提出的这个协议使用一个质数p的整数模n乘法群以及其原根g。下面展示这个算法，绿色表示非秘密信息, 红色粗体表示秘密信息：

爱丽丝和鲍伯最终都得到了同样的值，因为在模p下gab{\displaystyle g^{ab}}和gba{\displaystyle g^{ba}} 相等。 注意a, b 和 g = g mod p 是秘密的。 其他所有的值 – p, g, g mod p, 以及 g mod p – 都可以在公共信道上传递。 一旦爱丽丝和鲍伯得出了公共秘密，他们就可以把它用作对称密钥，以进行双方的加密通讯，因为这个密钥只有他们才能得到。 当然，为了使这个例子变得安全，必须使用非常大的a, b 以及 p， 否则可以实验所有gabmod23{\displaystyle g^{ab}{\bmod {23}}}的可能取值(总共有最多22个这样的值, 就算a和b很大也无济于事)。 如果 p 是一个至少 300 位的质数，并且a和b至少有100位长， 那么即使使用全人类所有的计算资源和当今最好的算法也不可能从g, p和g mod p 中计算出 a。这个问题就是著名的离散对数问题。注意g则不需要很大, 并且在一般的实践中通常是2或者5。IETF RFC3526 文档中有几个常用的大素数可供使用。

以下是一个更为一般的描述:

爱丽丝和鲍伯写上一个有限循环群G 和它的一个生成元g。 （这通常在协议开始很久以前就已经规定好； g是公开的，并可以被所有的攻击者看到。）

爱丽丝选择一个随机自然数a 并且将gamodp{\displaystyle g^{a}{\bmod {p}}}发送给鲍伯。

鲍伯选择一个随机自然数 b 并且将gbmodp{\displaystyle g^{b}{\bmod {p}}}发送给爱丽丝。

爱丽丝 计算(gb)amodp{\displaystyle \left(g^{b}\right)^{a}{\bmod {p}}}。

鲍伯 计算(ga)bmodp{\displaystyle \left(g^{a}\right)^{b}{\bmod {p}}}。

爱丽丝和鲍伯就同时协商出群元素gab{\displaystyle g^{ab}}，它可以被用作共享秘密。(gb)a{\displaystyle \left(g^{b}\right)^{a}}和(ga)b{\displaystyle \left(g^{a}\right)^{b}}因为群是乘法交换的。 (见幂.)

图示

下面的图示可以方便你理解每个信息都只有谁知道。（伊芙是一个窃听者—她可以看到爱丽丝和鲍伯的通讯内容，但是无法改变它们）

Let s = 共享密钥。 s = 2

Let a = 爱丽丝的私钥。如 a = 6

Let A = 爱丽丝的公钥。如 A = g mod p = 8

Let b = 鲍伯的私钥。如 b = 15

Let B = 鲍伯的公钥。如 B = g mod p = 19

Let g = 公共原根。如 g=5

Let p = 公共质数. 如 p = 23

注意：对爱丽丝来说解开鲍伯的私钥或鲍伯要解开爱丽丝的私钥应该都很困难。如果对爱丽丝来说解开鲍伯的私钥不难的话（反之亦然），伊芙可以轻易地替换掉她自己的私钥/公钥对，把鲍伯的公钥插到她自己的私钥，产生出一个假的共享密钥，并解开鲍伯的私钥（然后用这个解开共享私钥。伊芙可以试着选择一个能让她轻松解开鲍伯的私钥的公钥/私钥对）。

安全性

在选择了合适的G和g时，这个协议被认为是窃听安全的。偷听者("Eve")可能必须通过求解迪菲－赫尔曼问题来得到g。在当前，这被认为是一个困难问题。如果出现了一个高效的解决离散对数问题的算法，那么可以用它来简化a或者b的计算，那么也就可以用来解决迪菲－赫尔曼问题，使得包括本系统在内的很多公钥密码学系统变得不安全。

G的阶应当是一个素数，或者它有一个足够大的素因子以防止使用Pohlig–Hellman算法来得到a或者b。由于这个原因，一个索菲热尔曼素数q可以用来计算素数p=2q+1，这样的p称为安全素数，因为使用它之后G的阶只能被2和q整除。g有时被选择成G的q阶子群的生成元，而不是G本身的生成元，这样g的勒让德符号将不会显示出a的低位。

如果Alice和Bob使用的随机数生成器不能做到完全随机并且从某种程度上讲是可预测的，那么Eve的工作将简单的多。

秘密的整数a和b在会话结束后会被丢弃。因此，迪菲－赫尔曼密钥交换本身能够天然地达到完备的前向安全性，因为私钥不会存在一个过长的时间而增加泄密的危险。

身份验证

在最初的描述中，迪菲－赫尔曼密钥交换本身并没有提供通讯双方的身份验证服务，因此它很容易受到中间人攻击。 一个中间人在信道的中央进行两次迪菲－赫尔曼密钥交换，一次和Alice另一次和Bob，就能够成功的向Alice假装自己是Bob，反之亦然。而攻击者可以解密（读取和存储）任何一个人的信息并重新加密信息，然后传递给另一个人。因此通常都需要一个能够验证通讯双方身份的机制来防止这类攻击。

有很多种安全身份验证解决方案使用到了迪菲－赫尔曼密钥交换。当Alice和Bob共有一个公钥基础设施时，他们可以将他们的返回密钥进行签名，也可以像MQV那样签名g和g；STS以及IPsec协议的IKE组件已经成为了Internet协议的一部分；当Alice和Bob共享一个口令时，他们还可以从迪菲－赫尔曼算法使用口令认证密钥协商，类似于ITU-T的建议X.1035。这已经被用作了G.hn的家庭网络标准。

参见

密码学主页

模算术

椭圆曲线迪菲-赫尔曼

公钥密码学

ElGamal加密算法

迪菲－赫尔曼问题

MQV

口令认证密钥协商

引用

Dieter Gollmann (2006). Computer Security Second Edition West Sussex, England: John Wiley & Sons, Ltd.

Non-Secret Encryption Using a Finite FieldMJ Williamson, January 21, 1974.

Thoughts on Cheaper Non-Secret EncryptionMJ Williamson, August 10, 1976.

New Directions in CryptographyW. Diffie and M. E. Hellman, IEEE Transactions on Information Theory, vol. IT-22, Nov. 1976, pp: 644–654.

Cryptographic apparatus and method Martin E. Hellman, Bailey W. Diffie, and Ralph C. Merkle, U.S. Patent #4,200,770, 29 April 1980

The History of Non-Secret EncryptionJH Ellis 1987 (28K PDF file) (HTML version)

The First Ten Years of Public-Key CryptographyWhitfield Diffie, Proceedings of the IEEE, vol. 76, no. 5, May 1988, pp: 560–577 (1.9MB PDF file)

Menezes, Alfred; van Oorschot, Paul; Vanstone, Scott (1997). Handbook of Applied Cryptography Boca Raton, Florida: CRC Press. ISBN 0-8493-8523-7. (Available online)

Singh, Simon (1999) The Code Book: the evolution of secrecy from Mary Queen of Scots to quantum cryptography New York: Doubleday ISBN 0-385-49531-5

An Overview of Public Key CryptographyMartin E. Hellman, IEEE Communications Magazine, May 2002, pp:42–49. (123kB PDF file)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。