-
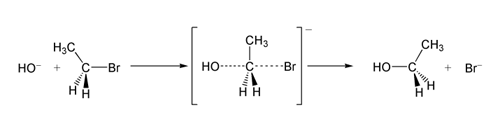
双分子亲核取代反应
反应机理SN2反应最常发生在脂肪族sp杂化的碳原子上,碳原子与一个电负性强、稳定的离去基团(X)相连,一般为卤素阴离子。亲核试剂(Nu)从离去基团的正后方进攻碳原子,Nu-C-X角度为180°,以使其孤对电子与C-X键的σ反键轨道可以达到最大重叠。然后形成一个五配位的反应过渡态,碳约为sp杂化,用两个垂直于平面的p轨道分别与离去基团和亲核试剂成键。C-X的断裂与新的C-Nu键的形成是同时的,X很快离去,形成含C-Nu键的新化合物。由于亲核试剂是从离去基团的背面进攻,故如果受进攻的原子具有手性,则反应后手性原子的立体化学发生构型翻转,也称“瓦尔登翻转”。这也是SN2反应在立体化学上的重要特征。反应过程类似于大风将雨伞由里向外翻转。溴乙烷与氢氧根离子发生SN2生成乙醇和溴离子。上例中,OH−(亲核试剂)进攻C2H5Br(底物)发生SN2反应,经过不稳定的过渡态,最终Br−离去,得到乙醇。SN2...
人物百科 | 2017-10-16 -

钷
性质物理性质钷原子中有61个电子,电子组态为[Xe]4f6s。在形成的化合物时,钷会失去其最外层的电子以及一个4f壳层电子,形成一个开放的子层。钷的原子半径在所有的镧系元素中排名第三,只稍微比相邻的元素大一点。钷有许多特性介于钕和钐的之间。例如熔点以及第一至第三电离能比钕大但比钐少;沸点及离子(Pm)和单原子气体的标准形成热比钐大但比钕少。钷具有双六方晶系密堆积(DHCP)结构,硬度63kg/mm。其加热至890℃时,会从常温的α形式转换成β形式(体心立方(bcc))。化学特性和化合物钷属于铈群镧系元素,其化性和相邻元素非常相近。由于钷非常不稳定,对于钷的化学研究并不完整,即使少部分的化合物已被合成,但它们亦没有被充分研究。一般来说,钷化合物通常是粉红色或红色。将含有Pm离子的酸与氨反应,会得出亮棕色的氢氧化钷(Pm(OH)3)凝胶状沉淀。将钷溶解在盐酸中,会产生一种水溶性的黄色盐类氯化钷...
人物百科 | 2017-10-16 -
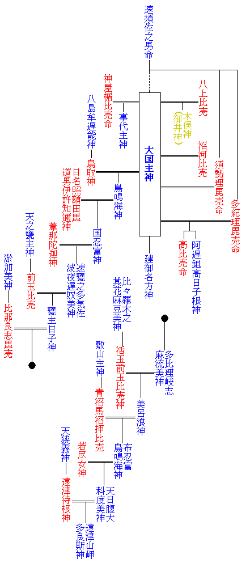
大国主
别称大国主拥有许多别名:大国主神(おおくにぬしのかみ)-统治大国的帝王之意大穴牟迟神(おおなむぢ)-大国主年轻时的名字大己贵命(おほなむち)-大国主年轻时的名字大汝命(おほなむち)-《播磨国风土记》中的称呼大物主神(おおものぬし)大穴持命(おおあなもち)大名持神(おおなもち)八千矛神(やちほこ)-矛是武力的象征,表示武神的性格苇原丑男・苇原色许男神(あしはらしこを)-表示武神的性格大国魂神(おほくにたま)显国魂神・宇都志国玉神(うつしくにたま)国作大己贵命(くにつくりおほなむち)・伊和大神(いわおほかみ)伊和神社主神-《播磨国风土记》中的称呼所造天下大神(あめのしたつくらししおほかみ)-《出云国风土记》中的尊称幽冥主宰大神(かくりごとしろしめすおおかみ)出自・事绩根据《日本书纪》本文,大国主是须佐之男命之子。在《古事记》、《日本书纪》之一书、《新撰姓氏录》书中,是须佐之男命之六世孙。在《日...
人物百科 | 2017-10-16 -

敏惠恭和元妃
人物简介敏惠恭和元妃(1609年-1641年),博尔济吉特氏,名海兰珠(蒙古名为乌尤塔)。科尔沁贝勒宰桑-布和之女,孝端文皇后侄女,孝庄文皇后姐姐。崇德元年(1636年),册封为宸妃,为四妃之首,赐居“关雎宫”。崇德二年七月初八日(1637年8月27日),宸妃生下皇太极第八子。皇太极为此下令大赦天下。但此子未来得及命名便早夭了。崇德六年(1641年),宸妃逝世,年三十三,谥曰“敏惠恭和元妃”,葬于清昭陵。博尔济吉特·海兰珠人物生平归嫁博尔济吉特·海兰珠(本名为乌尤塔),博尔济吉特氏,生于万历37年(1609年),她是孝庄文皇后的亲姐姐,比孝庄文皇后大4岁。海兰珠嫁给皇太极的时候已经26岁,比孝庄文皇后晚嫁皇太极9年。但是没有史料记载海兰珠26岁之前的资料。《清入关前内国史院满文档案》记载:“天聪八年(1634年)十月十六日。科尔沁部乌克善洪台吉率诸臣送妹至。汗偕诸福晋迎至,设大宴纳之为福晋...
人物百科 | 2017-10-16 -
刀狩令
刀狩令的背景武士刀被神社视为神圣的神体,并且把武士刀作为信仰的对象。和一般的观念不同的是,基本上没有武士在骑马的时候挥舞刀或者枪,也没有骑马的刀刃战,唯一的是最初骑马弓兵使用的刀。不过早期的武士以刀为武力为象征,信长,秀吉以及家康对刀的使用超过了战力的需要,收集名刀,在太平洋战争后存在500万武士刀,武士刀的精神意义不是单单的武器所能表现出来的。16世纪,近畿以及关东的平民在15岁的成人礼时,会得到一把胁差,允许携带刀的另一阶级是所谓的“小农民”,他们时常参加追捕落败武士,也就是通常所说的落武者狩。关东的后北条氏动员令要求人们自己负担弓,枪以及铁炮。因此,农村的村民就有机会参与战斗。在日本的中世和近世,农民腰上的东西是不可侵犯的。16世纪和17世纪的村落争斗中,夺取对方的胁差是重大的罪行。中世以来,刀象征着农民的武装权以及成年男性的人格和名誉。夺取农民手上的刀,自然就成为了大问题。丰臣氏的...
人物百科 | 2017-10-16 -
伽蓝神
佛陀时代之伽蓝神伽蓝菩萨系原本指记载于《七佛八菩萨大陀罗尼神咒经》的十八位护法伽蓝圣众:“护僧伽蓝神斯有十八人各各有别名。一名美音。二名梵音。三名天鼓。四名巧妙。五名叹美。六名广妙。七名雷音。八名狮音。九名妙美。十名梵响。十一名人音。十二名佛奴。十三名叹德。十四名广目。十五名妙眼。十六名彻听。十七名彻视。十八名遍观”等十八名护法天神。后来祇园精舍的三位功臣──舍卫国的国王波斯匿王(梵名:Prasenajit,巴利名:Pasenadi)、祇陀太子,及给孤独长者(Anathapindik,又名Sudatta〔须达多〕,意为“善授”)因为捐赠“祇树给孤独园”给释迦牟尼佛,于是也被列入伽蓝圣众之列,使伽蓝圣众增至二十一位。中国佛教供奉传统中国唐宋时,禅宗道场已有供奉伽蓝菩萨的风俗。《释氏要览》云:“寺院既有十八神护,居住之者,亦宜自励,不得怠惰为非,恐招现报耳。”又云:“一切神皆有无数眷属,即是分...
人物百科 | 2017-10-16 -
香积寺之战
背景虽然依靠唐玄宗的决策失误,安史叛军取得了灵宝之战的大捷,一举攻克长安。但由于唐朝长期将精锐部队集中在西北边境,这使得安史叛军虽然攻克了长安,但依然没有完全粉碎唐军的主力。到了757年时,大批原本不在内地的精锐边军,从安西、河西、北庭、朔方的军营赶到,令唐朝中央的军力得到恢复,拥有了和叛军角力的资本。同时,唐朝在内地又增设了额外的节度使,期望招募更多的新军。只是考虑到先前在洛阳和潼关的糟糕表现,皇帝与将军们都对这些新募部队没有太大期望。相比之下,安史集团的叛军本身也是良莠不齐的大杂烩。在安禄山不断扩充地盘的阶段,他们也以原来的契丹、同罗部队为核心,四处招兵买马。由于需要不断分兵到关中、山西、睢阳(今河南省商丘市)三条战线上进行消耗,导致安史叛军的战斗力迅速下滑。公元757年初,完成集结的唐军正式拉开了反攻大幕。但各边区军镇之间彼此之间的协同很成问题。在清渠之战中,叛军就利用骑兵猛攻唐军阵
人物百科 | 2017-10-16 -
光禄大夫
历史中国汉代初期分为中大夫、太中大夫、谏大夫。汉武帝时改中大夫为光禄大夫,秩比二千石,为掌议论之官,大夫中以光禄大夫最显要,西汉后期,九卿等高官多由光禄大夫升迁上来。晋代始于光禄大夫外加置左光禄大夫及右光禄大夫。隋炀帝以九大夫和“八尉”十七阶构成本阶,九大夫即:光禄大夫,从一品;左光禄大夫,正二品;右光禄大夫,从二品;金紫光禄大夫,正三品;银青光禄大夫,从三品;正议大夫,正四品;通议大夫,从四品;朝请大夫,正五品;朝散大夫,从五品。唐代、宋代以后成阶官之名,为从二品官员。元代又升为从一品,明代以特进光禄大夫为文职散官最高官阶。清代顺治年间文职正从一品均称光禄大夫,在光禄大夫前加“特进”二字,为正一品官,是文臣最高阶官。朝鲜越南琉球参考文献
人物百科 | 2017-10-16 -
阿尔弗雷德·布莱洛克
早年生活和事业早期阿尔弗雷德·布莱洛克在1899年出生于美国佐治亚州门罗县卡洛登(英语:Culloden,Georgia)。他的母亲是玛莎·(戴维斯)·布莱洛克,父亲乔治·泽多克·布莱洛克是一位商人。14岁时,布莱洛克进入佐治亚大学的预科学校佐治亚军事学院(英语:GeorgiaMilitaryAcademy)学习,之后进入了佐治亚大学。1918年,19岁的布莱洛克从大学毕业,获得了文学士学位并进入了约翰·霍普金斯大学医学院学习。在医学院期间,他与室友廷斯利·哈里森(英语:TinsleyHarrison)结下深厚友谊,两位医生之后也成为了一生的挚友。1922年,布莱洛克从约翰霍普金斯大学获得医学博士学位。布莱洛克敬仰约翰·霍普金斯医院的创始人、美国外科学先驱威廉·史都华·豪斯泰德,于是在毕业后给他写信,希望在他手下实习,却没能如愿。但布莱洛克仍然留在巴尔的摩,在约翰·霍普金斯大学的泌尿外科完...
人物百科 | 2017-10-16 -
无处稠密集
定义拓扑空间(X,τ),A⊆X,称A是无处稠密的(亦称稀疏的,或称A为无处稠密集、稀疏集),当且仅当A的闭包的内部是空集。例子例如,整数在实数轴R上就形成了一个无处稠密集。注意运算的次序是很重要的。例如,有理数的集合,由于是R的子集,因此它的内部的闭包(注意不是“闭包的内部”)是空集,但不是无处稠密集;实际上,它在R上是稠密的,正好相反。无处稠密与周围的空间也有关:有可能把一个集合考虑为X的子空间时就是无处稠密的,但考虑为Y的子空间时,就不是无处稠密的。显然,一个集合在它本身中总是稠密的。开集和闭集一个无处稠密集不一定是闭集(例如,集合{1,1/2,1/3,……-->}{\displaystyle\{1,1/2,1/3,\dots\}}在实数集上是无处稠密集),但一定是包含在一个无处稠密的闭集(即它的闭包)内。确实,一个集合是无处稠密集,当且仅当它的闭包是无处稠密集。无处稠密的闭集的补集是...
人物百科 | 2017-10-16




